А.А.Проскурнин

 

Математические модели
оценки знаний

 

Введение

В настоящее время существует множество самых разных математических моделей и подходов, описывающих те или иные стадии процесса контроля знаний, и опирающихся на различные разделы математики. Используются теория вероятности и математическая статистика, теория графов, теория нечетких множеств и нечеткая логика, теория латентно-структурного анализа, теория принятия решений и исследование операций, комбинаторная топология и теория фракталов и многое другое.

Для интеллектуальных систем контроля знаний математическое моделирование сопрягается с информационным моделированием и использованием различных моделей знаний.

В этой статье сделана попытка классифицирования и описания основных математических моделей (подходов, методов), применяемых для оценки знаний. Нужно уточнить, что здесь не рассматривается множество математических моделей, которые используются в контроле знаний, но не являются непосредственно моделями оценки знаний – например, модели проведения контроля, в частности, адаптивное тестирование, модели оценки качества тестов и т.д.

В соответствии с педагогическим энциклопедическим словарем под редакцией [Б.М. Бим-Бада], проверка и оценка знаний, умений и навыков учащихся – это процесс выявления и сравнения на том или ином этапе обучения результатов учебной деятельности с требованиями, задаваемыми учебными программами; выражается в форме отметки (в баллах) или словесного (оценочного) суждения учителя.

Модели оценки знаний можно разделить на три больших класса: модели оценки уровня знаний, модели диагностики знаний и модели распознавания (классификации). Классификация моделей оценки знаний показана на рис.1.

Модели оценки уровня знаний направлены на получение интегральной, количественной оценки испытуемого, так называемого балла. Модели диагностики позволяют выявить пробелы, характерные ошибки в знаниях; вместо интегральной оценки они предполагают оценивание различных учебных элементов (дидактических единиц) изучаемого курса или раздела. Модели распознавания (классификации) ставят своей целью отнести испытуемого по результатам тестирования к одному из заранее определенных классов, например, класс «аттестован» и класс «не аттестован».

На рис.1 для каждого из трех классов моделей оценки знаний приведены отдельные модели или совокупности моделей, основанные на определенном подходе, методе. Рассмотрим эти модели более подробно.

 

Модели оценки уровня знаний

Простая модель. Данная модель является самой простой и самой распространенной. Ответ студента на каждое задание оценивается по двухбалльной (правильно или неправильно) или многобалльной (например, пятибалльной) шкале. Оценка выставляется путем вычисления значения R [Зайцева Л.В]:

,

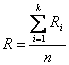где R_i – правильный ответ обучаемого на i-е задание; k – количество правильных ответов из n предложенных (k <= n), которое затем обычно округляется по правилам математики.

Окончательная оценка, как правило, определяется по формуле:

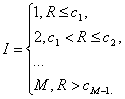
Здесь I – окончательная оценка, {c₁, c₂, …, c_M} – вектор граничных значений, M – максимально возможная оценка (например, при пятибалльной шкале M = 5).

К достоинствам данной модели следует отнести простоту ее реализации. Недостатком модели является ее зависимость от единственного параметра (количества правильных ответов), т.е. она не учитывает не полностью точные ответы и характеристики заданий. Простейшая модель имеет самую низкую надежность, т.к. не позволяет объективно оценить знания студента.

 

 

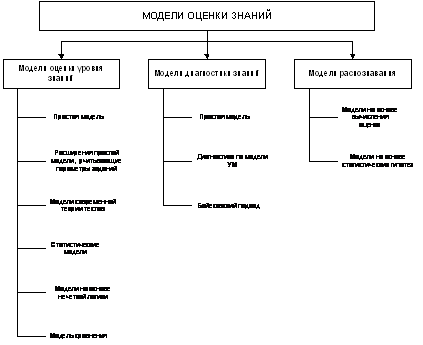
Рис. 1. Модели оценки знаний

 

Расширения простой модели, учитывающие параметры заданий. В этих моделях при выставлении оценки используются характеристики контрольных вопросов. Существуют различные модификации данного типа моделей. Рассмотрим некоторые из них [Зайцева Л.В].

1. Модель, учитывающая время выполнения задания и/или общее время контрольной работы. Для правильных ответов рассчитывается значение R_i по формуле:

,

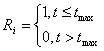где t – время выполнения задания, t_max – время, отведенное для выполнения задания.

Далее итоговая оценка выставляется аналогично «Простой модели».

2. Модель на основе уровней усвоения. В этой модели характеристикой задания является уровень усвоения, для проверки которого оно предназначено. Таким образом, задания разделяются на пять групп, соответствующих уровням усвоения: понимание, опознание, воспроизведение, применение, творческая деятельность. Для каждого задания определяется набор существенных операций. Под существенными понимают те операции, которые выполняются на проверяемом уровне. Операции, принадлежащие к более низким уровням, в число существенных не входят. Для выставления оценки используется коэффициент К_a:

,  ,

где P₁ – количество правильно выполненных существенных операций в процессе контроля; Р₂ – общее количество существенных операций в контрольной работе; a = 0, 1, 2, 3, 4 – соответствуют уровням усвоения. Оценка выставляется на основе заданных граничных значений по соотношениям:

§      K_a < 0.7 – неудовлетворительно;

§      0.7 <= K_a < 0.8 – удовлетворительно;

§      0.8 <= K_a < 0.9 – хорошо;

§      K_a >= 0.9 – отлично.

3. Метод линейно-кусочной аппроксимации. Алгоритм оценивания основан на классификации заданий (вопросов) по их дидактическим характеристикам (значимость (z), трудность (d), спецификация (s)). Число баллов, полученных студентом за выполнение n заданий, определяется по формуле:

,

где x_i – оценка за выполнение i-го задания; n – число заданий; W = {w_i} – вектор весовых коэффициентов заданий, зависящий от их дидактических характеристик.

По завершению контроля определяется средний балл А, полученный студентом за выполнение n заданий (A = y / k_n, где k_n – количество попыток выполнения n заданий, k_n >= n ) и уточненный средний балл A':

, где:

r – ранг обучаемого (1, 2, или 3); k_n – количество попыток выполнения n заданий; k_c – количество обращений к справочной информации; k_b – количество заданий, выполненных с превышением отведенного времени (k_b <= n); a₁, a₂, a₃, a₄ – коэффициенты.

Далее значения уточненного среднего балла с помощью вектора граничных значений переводятся в обычную пятибалльную шкалу.

Параметры контроля, а именно значения весовых коэффициентов w_i, коэффициентов a_i и значения элементов вектора граничных значений определяются на этапе обучения по результатам контрольного эксперимента.

 

Модели современной теории тестов. Под современной теорией тестов здесь понимается существующая на Западе Item Response Theory (IRT), предназначенная для оценки латентных параметров испытуемых и параметров заданий теста посредством применения математико-статистических моделей измерения [Челышкова М.Б.].

В отличие от классической теории, где индивидуальный балл тестируемого рассматривается как постоянное число, в IRT латентный параметр трактуется как некоторая переменная. Начальное значение параметра получается непосредственно из эмпирических данных тестирования. Переменный характер измеряемой величины указывает на возможность последовательного приближения к объективным оценкам параметра с помощью тех или иных итерационных методов.

В рамках основного предположения IRT устанавливается связь между латентными параметрами испытуемых и наблюдаемыми результатами выполнения теста. При установлении связи важно понимать, что первопричиной являются латентные параметры. Если говорить точно, то взаимодействие двух множеств значений латентных параметров порождает наблюдаемые результаты выполнения теста.

Элементы первого множества – это значения латентного параметра, определяющего уровень подготовки N испытуемых q_i (i = 1, 2, .., N). Второе множество образуют значения латентного параметра b_j (j = 1, 2, …, n ), равные трудностям n заданий теста.

Однако на практике всегда ставится обратная задача: по ответам испытуемых на задания теста оценить значения латентных параметров q и b. Для ее решения нужно ответить по меньшей мере на два вопроса.

Первый связан с выбором вида соотношения между латентными параметрами q и b. Идея установления соотношения принадлежит датскому математику Г. Рашу, который предложил ввести его в виде разности (q - b), предполагая, что параметры q и b оцениваются в одной и той же шкале.

Ответ на второй вопрос, который является центральным в IRT, связан с выбором математической модели для описания рассматриваемой связи между латентными параметрами и наблюдаемыми результатами выполнения теста.

В частности, можно рассматривать условную вероятность правильного выполнения i-м испытуемым с уровнем подготовки q_i различных по трудности заданий теста, считая q_i параметром i-го ученика, а b – независимой переменной. В этом случае условная вероятность будет функцией латентной переменной b:

, i = 1, 2, …, N.

 Здесь x_ij = 1, если ответ i-го испытуемого на j-е задание верный; x_ij = 0, если ответ i-го испытуемого на j-е задание неверный.

Аналогично вводится условная вероятность правильного выполнения j-го задания с трудностью b_j различными испытуемыми группы. Здесь независимой переменной является q, а b_j – параметр, определяющий трудность j-го задания теста:

, j = 1, 2, …, n.

В теории IRT функции f(b) и j(q) получили название Item Response Functions (IRF). Специальное название имеют и их графики. График функции P_j – это характеристическая кривая j-го задания (ICC), а график функции P_i – индивидуальная кривая i-го испытуемого (PCC).

При выборе вида функций P_i и P_j учитываются обстоятельства как эмпирического, так и математического характера. В предположении нормального распределения значений латентных переменных q и b таких функций предлагаются две. Одна из них, обычно обозначаемая y(x), относится к семейству логистических кривых, другая Ф(x), является интегральной функцией нормированного нормального распределения. Поскольку для одних и тех же значений x ординаты точек графиков функций Ф(x) и y(1,7x) отличаются друг от друга достаточно мало, то в том, что их две, нет ни ошибки, ни противоречия. А именно, для всех x, принадлежащих области определения этих функций,

|Ф(x) - y(1,7x)| < 0,01.

Наиболее сильный аргумент в пользу логистической функции связан не с качеством измерений, а с относительной простотой ее аналитического задания, выгодной при оценивании параметров q и b. Поэтому в практических приложениях предпочтение обычно отдают функции y(1,7x).

Число параметров, входящих в аналитическое задание функций, является основанием для подразделения семейства IRF на классы. Среди логистических функций различают:

однопараметрическую модель Г. Раша

,

,

где q и b – независимые переменные для первой и второй функций соответственно.

двухпараметрическую модель А. Бирнбаума

,

 

.

Кроме прежних обозначений в этой модели появляются параметры a_i и a_j. Параметр a_j был введен А. Бирнбаумом для характеристики дифференцирующей способности задания при измерении различных значений q; параметр a_i указывает на меру структурированности знаний ученика.

трехпараметрическую модель А. Бирнбаума

,

где c_j является третьим параметром модели, характеризующим вероятность правильного ответа на задание j в том случае, если этот ответ угадан, а не основан на знаниях ученика.

В каждой из представленных моделей параметры q и b выражаются как шкалированные показатели единой для всех моделей шкалы логитов. При отношении двух величин, равном е, их различие составит 1 логит. Таким образом, получается шкала, в которой можно говорить, что знания двух испытуемых или трудности двух упражнений различаются на столько-то логит (а не во столько-то раз).

Начальные значения параметров q и b находят по формулам:

,

,

где p_i и q_i – доли правильных и неправильных соответственно ответов i-го ученика на задания теста; p_j и q_j – доли правильных и неправильных ответов учеников на j-е задание теста.

Затем начальные значения параметров переводятся в единую интервальную шкалу стандартных оценок. Стандартизация достигается с помощью ряда специальных преобразований, в ходе которых вычисляются среднее значение  для множества (i =  1, 2, …, N), среднее значение  для множества (j = 1, 2, …, n), дисперсии по этим множествам и поправочные коэффициенты X и Y. Оценки параметров q и b в единой интервальной шкале находятся по формулам:

,

.

Роль последних двух формул в развитии современной теории тестов трудно переоценить, хотя на первый взгляд они имеют узкую практическую направленность. Эти формулы позволяют преодолеть ряд существенных недостатков классической теории тестов, поскольку с их помощью можно получить объективные оценки параметров испытуемых и заданий, не зависящие друг от друга и выраженные в единой интервальной шкале.

Хотелось бы напомнить еще раз о важном преимуществе полученных оценок параметров q и b. Благодаря особенностям математического аппарата IRT проведенные расчеты обеспечивают объективные оценки уровня подготовки каждого испытуемого, не зависящие от трудности заданий теста. Отмеченное свойство инвариантности позволяет провести корректное сравнение результатов испытуемых, выполнивших различные по трудности задания теста и даже разные тесты.

Аналогичное преимущество существует в IRT и для оценок трудности заданий теста. Получаемые по алгоритмам значения параметра b инвариантны относительно уровня подготовки испытуемых в тестируемой группе.

Хотя теория обещает инвариантность, в силу действия различных случайных факторов оценки параметров q и b, полученные на нескольких выборках, будут, конечно, различаться. Если объем выборки достаточно велик, то можно ставить вопрос о вычислении устойчивых значений параметров q и b, которые будут наиболее эффективными оценками и могут быть приняты в качестве объективных значений q и b. Например, для вычисления таких эффективных оценок можно использовать метод наибольшего правдоподобия, предложенный Р.Фишером.

Статистические модели. В этих моделях для получения оценки испытуемого используют методы теории вероятности и математической статистики. В целом, теория вероятности и математическая статистика используются очень широко для анализа результатов тестирования. Ранее уже были рассмотрены элементы статистической теории обучения и контроля знаний. Вероятностный подход использует и теория IRT, и классическая теория тестирования.

В качестве примера статистической модели оценивания рассмотрим метод, предложенный Рудинским И.Д. и Грушецким С.В. в работе [Рудинский И.Д.]. Основная идея данного метода заключается в том, что, при достаточно большом объеме тестовой выборки, предъявляемой обучаемому (с количеством тестовых заданий не менее 50), функции распределения ответов обучаемых, характеризующихся различным уровнем знаний, тяготеют к вполне определенным законам распределения.

Так, при наличии полных и глубоких знаний распределение ответов близко к экспоненциальному с параметром 1, а при практически полном их отсутствии – к экспоненциальному с параметром 0. Если обучаемый демонстрирует не отличные, но ровные и уверенные знания по всей области покрытия теста, то распределение его ответов будет близко к нормальному с отчетливо выраженным максимумом и относительно небольшой дисперсией, тогда как при наличии значительных пробелов по отдельным темам это распределение будет близко к нормальному с незначительно выраженным максимумом и большой дисперсией. В то же время, при попытке угадывания правильных ответов (т.е. при их случайном выборе) распределение будет близко к равномерному.

Основная идея предлагаемого в работе алгоритма заключается в следующем. При проведении автоматизированного тестирования знаний с учетом выбранных обучаемым вариантов ответа полученные ответы группируются и строится полигон частот их распределения. Последовательно выдвигаются нулевые и альтернативные им гипотезы об экспоненциальном, нормальном и равномерном распределении совокупности ответов. Выдвинутые гипотезы проверяются с помощью соответствующих критериев согласия, причем для дальнейшего анализа выбирается та гипотеза, степень согласия с которой оказывается наибольшей. С учетом параметров принятого закона распределения, объема выборки и требуемой доверительной вероятности рассчитывается величина доверительного интервала, которая проецируется на эталонную оценочную шкалу для выбора итоговой оценки. В случае, если доверительный интервал полностью помещается в области, расположенной между двумя соседними оценками, то выставляется более высокая из них. Ситуация, в которой доверительный интервал перекрывает области двух соседних оценок, свидетельствует о недостаточной определенности результатов тестирования. Эта неопределенность может быть снята либо предъявлением обучаемому дополнительных тестовых заданий с последующим повторением расчета при увеличенном объеме выборки, либо выставлением более низкой оценки, соответствующей общей границе перекрытых областей.

Статистические методы применяются также для оценки качества тестов, достоверности тестирования, прогнозирования результатов испытуемых.

Модели на основе нечеткой логики. Применение нечеткой логики – это одно из направлений интеллектуализации систем контроля знаний. Имеются различные модификации данного подхода.

Например, это переход от задания истинности предлагаемых вариантов ответов в категориях двоичной логики (“правильно — неправильно”) к более общей и универсальной схеме оценивания ответов функциями принадлежности, определяемыми в категориях нечеткой логики. Такой переход не отрицает и традиционный подход, поскольку в соответствии с современными представлениями двоичная логика может считаться частным (точнее, вырожденным) случаем нечеткой логики.

В работе [Михаль О.Ф.] предложена модель оценивания знаний на основе локально-параллельных нечетких алгоритмов.

Модель сравнения. Основная идея этой модели заключается в следующем. Для того, чтобы оценить систему приобретенных обучаемым знаний, необходимо сравнить модель системы знаний обучаемого и эталонную модель структуры предмета с целью установления аналогии (сходства) между ними. Если аналогия существует, то вычисляется степень аналогии для определения оценки системы знаний обучаемого в рамках этого предмета. 

При этом модели системы знаний обучаемого и эталонной структуры предмета представляют собой, как правило, графы (семантические сети). Система, реализующая данный подход, описана в работе [Калашникова Т.Г.].

 

Модели диагностики знаний

Простая модель. В простой модели диагностики знаний тестовые задания связываются с дидактическими единицами (учебными элементами, тематическими единицами) предмета, по каждой из выбранных заранее для тестирования дидактических единиц обучаемому предлагается определенное число заданий. Результатом контроля является список дидактических единиц, для каждой из которых вычисляется процент верно выполненных заданий.

Диагностика по модели УМ (учебного материала). Эта модель, в отличие от простой модели диагностики, предполагает более сложное представление модели изучаемого предмета и более сложные алгоритмы работы с этой моделью.

Рассмотрим эту модель более подробно на примере системы, описанной в работе [Андреев А.Б.]. Суть метода состоит в создании формальной системы знания о структуре учебного материала и уровнях сложности отдельных его структурных элементов. Реализация заключается в структуризации учебного материала и разработке компонентов системы. В рамках системы разрабатываются:

·      Модель представления знаний об учебном материале.Учебный материал рассматривается как система знаний, состоящая из понятий и отношений между ними, отражающими знания о структурных свойствах учебного материала и уровнях сложности. Модель знаний о структуре изучаемого учебного материала представляется в виде семантической сети.

·      База знаний и средства ее наполнения. Знания в экспертной системе представляются в декларативной и процедуральной формах. В декларативной форме представлена семантическая сеть. В базе знаний семантической сети содержатся: описание понятий; отношения "определения" и "уровень сложности" между понятиями; тестовые вопросы для каждого понятия с несколькими вариантами ответов. В процедуральной форме представлены процедуры построения дерева поиска и нахождения результата. При этом используются следующие процедуры: обход графа сети; анализ знания понятия; вычисление оценки и получение "фотографии знаний".

·      Экспертную систему, позволяющую на основе существующей базы знаний и ответов студентов логически выводить оценку и формировать очередное задание. Экспертная система предназначена для анализа знаний обучающегося, а именно для определения упорядоченной совокупности известных и неизвестных ему понятий ("фотография знаний") и вычисления общей оценки знаний. Основная стратегия управления дедуктивным механизмом вывода - обратная цепочка рассуждений. Исходная цель – доказательство истинности утверждения "понятие известно" для понятия самого верхнего уровня, соответствующего анализируемой теме.

Диагностика знаний на основе байесовского подхода. Данная модель подробно описана в работе [Атанов Г.А.]. Предлагается следующий алгоритм для построения диагностирующей экспертной системы:

1.    Выбрать задачу (или тему) P1, на основе которой будет осуществляться диагностика.

2.    Определить те знания и умения (объекты, ситуации, отношения, требования, операторы), которые необходимы обучаемому для решения задачи P1 (или что он должен знать и уметь после изучения выбранной темы). Иными словами, разбить задачу P1 на элементарные подзадачи, решая которые можно последовательно перебрать спектр исходной задачи или темы, поскольку спектр исходной задачи (темы) и суммарный спектр подзадач должны совпадать.

3.    Исходя из суммарного спектра, составить список гипотез вида "обучаемый не знает/не умеет" и вида "обучаемый знает/умеет".

4.    Составить текст предписания для каждой гипотезы.

5.    Определить множество симптомов вида "обучаемый знает/умеет".

6.    Установить соответствие между симптомами и подзадачами, при решении которых эти симптомы означиваются. При этом все симптомы должны означиваться хотя бы одной задачей (см. п. 2).

7.    Составить таблицу соответствия "гипотезы - симптомы".

8.    Определить априорные вероятности гипотез.

9.    Определить вероятности подтверждения и опровержения гипотез симптомами.

10.     Наполнить базу знаний экспертными и предметными знаниями.

В процессе тестирования используется механизм байесовского вывода; результатом тестирования являются апостериорные вероятности для каждой из гипотез вида "обучаемый не знает/не умеет" и вида "обучаемый знает/умеет".

Априорные вероятности гипотез, вероятности подтверждения и опровержения гипотез симптомами являются экспертными знаниями. Они, как правило, определяются экспериментально.

 

 Модели распознавания (классификации)

Модели на основе вычисления оценок. Алгоритм, основанный на вычислении оценок (АВО) был впервые предложен Ю.И. Журавлевым и позднее использовался для классификации обучаемых по уровням подготовленности и для оценки знаний в качестве дополнительного метода в обучающих системах [Зайцева Л.В]. Данная модель предусматривает построение таблицы обучения Т^о_nm, в которой каждая строка представляет собой набор признаков обучаемого характеризующих работу студента в процессе контроля знаний: количество предложенных заданий (n), средний балл (A), количество попыток выполнения заданий (k_n), количество обращений к справочной информации (k_c), ранг (r). При выставлении оценки вычисляется степень похожести совокупности признаков конкретного студента I(S) = {b₁, b₂, …, b_m} на строки, входящие в таблицу обучения Т^о_nm, на основании чего осуществляется отнесение его к определенному классу K_j. Для этого вычисляется число строк каждого класса K_j, близких по выбранному критерию классифицируемому объекту S. Строка таблицы обучения Т^о_nm I(S^j_i) = {a ^j_i1, …, a^j_im} и распознаваемая строка I (S) = {b₁, b₂, …, b_m} считаются похожими, если выполняются неравенства |a^j_ik –b_k| <= e_k, где e_k (k =1, …, m) - точность сравнения. Студент относится к классу K_j, имеющему максимальную оценку max Г_j (S, K_j), j = 1, …, m. Данная модель в настоящее время применяется также в модифицированном варианте: вместо одной таблицы обучения, содержащей данные для различных классов, используются четыре таблицы обучения для классов “отлично”, “хорошо”, “удовлетворительно” и “неудовлетворительно”, названные эталонными таблицами оценивания.

Модели на основе статистических гипотез. В этой модели полагается, что существует два основных вида распределений вероятностей оценок уровня учебных достижений: биномиальный и нормальный [Васильев В.И.].

В результате тестирования относительное описание поведения обучаемого состоит из выборки в виде N-разрядного кода, включающей в себя заключения (ответы) обучаемого на тестовые задания (0 – неверный ответ, 1 – верный ответ). Взяв сумму значений признака этой выборки, можно установить оценку уровня достижений тестируемого. С точки зрения отнесения его к тому или иному классу обученности существенно следующее: превышает или не превышает эта сумма величину некоторым образом сформированного оптимального порога обученности тестируемого.

Для выбора этого оптимального порога решения используются известные в теории статистических гипотез критерии. При этом учитывается, что количество заданий в тесте может быть фиксированным или определяться программой тестовых испытаний. Алгоритмы классификации тестируемых являются оптимальными, так как базируются на критериях, обеспечивающих или минимальную ошибку принятия решения при фиксированной выборке (критерии Байеса, Неймана-Пирсона, минимакса), или минимальную выборку наблюдений при заданных ошибках принятия решений (критерий Вальда).

 

Литература

 

1.	[Б.М. Бим-Бад.]
2.	[Челышкова М.Б.]
3.	[Рудинский И.Д.]
4.	[Михаль О.Ф.]
5.	[Калашникова Т.Г.]
6.	[Андреев А.Б.]
7.	[Атанов Г.А.]
8.	[Зайцева Л.В]
9.	[Васильев В.И.]
10.	[Прокофьева Н.О.]