На практике довольно часто приходится сталкиваться с необходимостью представления результатов решения какой-либо сложной задачи или некоторого исследования в удобном для восприятия человека виде. На данный момент существует множество путей достижения этой цели, и во многих ситуациях, особенно для сложных, комплексных задач, наилучшим решением является графическое представление. Одним из важнейших его преимуществ является наглядность и простота восприятия представляемой информации.
Задача графического представления результатов не всегда проста, ведь она редко сводится к построению ряда графиков и схем, которые можно быстро и с высоким качеством сделать в обыкновенном графическом редакторе. В статье приводится лишь один пример из целого класса весьма сложных задач по графическому отображению собранной информации и набор общих методов и алгоритмов, которые потребуются для ее решения.
Начнем примера. Предположим, что необходимо отобразить радиационную ситуацию на какой-либо территории. Исходными данными для решения задачи являются результаты проведенных на этой территории измерений радиационного фона. Уже здесь намечается первая проблема: измерения можно провести только в некоторых точках, а поставленная задача требует отображения ситуации на всем протяжении выбранной территории. Фактически, требуется перевести некоторое число дискретных значений на непрерывное пространство. У подобной задачи может существовать более одного решения, причем возможно, что все решения будут правильными. Поэтому, прежде чем отыскивать алгоритм для решения этой задачи, попытаемся представить себе, какое бы ее решение нас удовлетворило.
Допустим, в качестве исходных данных у нас есть n (n = 5) точек и некоторая область A (рис. 1).
У каждой точки есть некоторой атрибут, который в нашем случае является значением радиационного фона в данной точке. Попробуем решить эту задачу для начала следующим растровым методом. Разобьем область А на m элементарных непересекающихся ячеек, аналогичных пикселям дисплея (потом мы отождествим эти ячейки пикселям). Затем будем последовательно перебирать каждую полученную ячейку и присваивать ей атрибут ближайшей к ней точки. Результат подобных действий будет представлять собой разбиение области А на непересекающиеся подобласти, ядром каждой из которых является одна из точек (рис. 2).
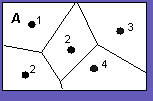
Необходимо заметить, что это далеко не единственно возможное разбиение области А, но оно представляется наиболее удачным и логичным для рассматриваемого класса задач.
Теперь, зная желаемый результат, необходимо разработать метод, позволяющий достигнуть его. Вполне законен вопрос: нужно ли разрабатывать какой-то иной метод, если мы уже имеем готовый и крайне простой алгоритм, правда, для растрового решения задачи? Дело в том, что у описанного выше растрового метода есть ряд существенных недостатков, основные из которых: сложность автоматической обработки результатов его работы и неудовлетворительное время работы.
Нетрудно посчитать, что время работы такого алгоритма будет лежать в диапазоне:
,
где х, у — количество элементарных ячеек по горизонтали и вертикали соответственно;
n — количество точек.
Очевидно, что для достижения хорошего качества изображения необходимо за элементарные ячейки брать пиксели дисплея, что при большом разрешении будет очень сильно влиять на временную характеристику алгоритма (ухудшать ее). С другой стороны, у этого алгоритма есть очень полезное свойство — линейная зависимость времени выполнения от количества точек-данных.
Попробуем теперь решить эту задачу в векторном виде, используя определения аналитической геометрии и линейной алгебры.
Определение 1. Скалярное произведение.
По определению скалярное произведение двух векторов равно:
.
В ортонормированном базисе скалярное произведение двух векторов равно сумме произведений одноименных координат. Следовательно, для двумерной декартовой системы координат имеем:
.
Скалярное произведение имеет ряд важных свойств:
) = (
);
;
справедливо следующее: 
;
& 
;
;
;
,
где 
— скалярная
величина;
Определение 2. Поворот вектора.
Рассмотрим поворот вектора
на 90 градусов по часовой стрелке вокруг своей
середины (рис. 3):
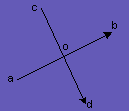
Точка O
будет иметь следующие координаты: 
,
а вектор, перпендикулярный
вектору 
= (
)
определяется как 
= (
).
Тогда координаты точек c
и d можно определить
следующим образом:
с 
,
d 
.
Определение 3. Нахождение точки пересечения двух прямых, каждая из которых задана двумя своими точками.
Предположим, что заданы две
прямые своими направляющими векторами 
и 
.
Тогда первую прямую (ее направляющий вектор
— )
можно описать следующим уравнением:
. (1)
Найдем теперь такое 
,
что заданные прямые пересекутся в точке 
.
Так как вектор 
параллелен вектору 
,
то 
и 
перпендикулярны одному и тому же вектору
.
Следовательно, на основании свойств 4 и 7 для
нахождения точки пересечения необходимо
решить следующее уравнение относительно
параметра t:
Подставляя в (2) выражение (1) получаем:
Из (3) можно легко найти искомое t:
. (4)
Параллельность двух заданных
прямых соответствует случаю, когда 
(обе прямые перпендикулярны одному и тому
же вектору). Перпендикуляр 
легче всего найти следующим образом:
. (5)
Подставив (4) и (5) в выражение (1), можно окончательно определить точку пересечения заданных прямых линий.
Теперь, возвращаясь к решению поставленной задачи, решим ее и в векторном виде так, чтобы результат совпадал бы с результатом, полученным при растровом методе решения.
На первом этапе предельно упростим задачу, предположив, что на нашей плоскости существуют только две точки. Кроме того, введем еще одно упрощение: будем рассматривать не всю бесконечную плоскость, а лишь некоторый прямоугольник, в который входят все рассматриваемые точки. Тогда очевидно, что плоскость должна быть разбита на две области, которые будут граничить по некоторой прямой, проходящей между двумя заданными точками (рис. 4).
Эту прямую нетрудно найти: она должна быть перпендикуляром к отрезку, соединяющему исходные точки и проходить через середину этого отрезка (см. Определение 2). Таким образом, эта прямая разбивает плоскость на области, совершенно аналогичные тем, которые могли бы быть получены при использовании описанного выше растрового метода.
Теперь будем постепенно усложнять задачу: вместо двух точек возьмем три (рис. 5). Построим область для точки 2: для этого дважды выполним только что описанную процедуру. Сначала разобьем прямоугольник на две области относительно точек 1 и 2 и назовем ту область, которой принадлежит точка 2 (другая область нас пока не интересует и как таковую строить мы ее на данном этапе не будем) “область A”. Теперь повторим эту процедуру относительно точек 2 и 3 и назовем ту область, которой принадлежит точка 2, “область B”. Мы получили две пересекающиеся области, пересечение которых и даст искомую область для точки 2. Такую же последовательность действий необходимо выполнить и для остальных точек: 1 и 3.
Здесь необходимо заметить, что, говоря об областях, имеются в виду многоугольники, описывающие их границу. Представление области в виде многоугольника позволяет свести все действия по их пересечению к ряду довольно простых математических преобразований. Кроме того, очевидно, что получаемые многоугольники будут выпуклыми. Это значительно упрощает все алгоритмы по их преобразованию.
Пусть теперь задано конечное множество F — множество точек на плоскости, и существует некоторая точка q на этой же плоскости, не принадлежащая множеству F. Тогда многоугольником Вороного, соответствующего точке q, относительно множества F называется множество точек плоскости, которые расположены к точке q ближе, чем к любой другой точке из множества F. Для каждой точки q из множества F множество точек плоскости, которые ближе к q, чем к p, соответствует полуплоскости, ограниченной перпендикуляром, проведенным через середину отрезка [p, q], причем эта полуплоскость должна содержать точку q. Многоугольник Вороного равен пересечению всех таких полуплоскостей, образованных точками из множества F (рис. 6).
Как уже отмечалось ранее, для реализации этого алгоритма необходимо наличие ограничивающего выпуклого многоугольника, в качестве которого для простоты можно взять прямоугольник или квадрат. Требование выпуклости ограничивающего многоугольника выдвинуто исключительно для упрощения реализации алгоритма, так как задача по пересечению двух произвольных многоугольников значительно сложнее, нежели задача по пересечению выпуклых многоугольников. Ограничивающий многоугольник должен быть достаточно большим, чтобы не потерять нужную информацию.
Ясно, что если построить многоугольник Вороного для каждой точки s из множества F относительно множества G=F/{s} (то есть все точки из F, кроме s), то будет получено искомое разбиение плоскости (в нашем случае прямоугольника) на области (рис. 7).
Рассмотрим теперь подробнее алгоритм формирования многоугольника Вороного. Этот многоугольник V(s), где s — точка, вокруг которой строится многоугольник, является результатом пересечения набора полуплоскостей H. Область V(s), безусловно, является выпуклым многоугольником, поскольку пересечение выпуклых областей всегда выпукло.
Одним из способов формирования пересечения n полуплоскостей будет их поочередная обработка. Область пересечения n полуплоскостей может быть получена попарным пересечением этих полуплоскостей в произвольном порядке, то есть набор полуплоскостей ассоциативен. Из этого следует, что при любом делении набора s на два непустых поднабора s1 и s2 будем иметь V(s) = V(s1)Ç V(s2). Таким образом, для вычисления V(s) необходимо разбить набор полуплоскостей s на два непустых поднабора s1 и s2 примерно одинакового размера, затем рекурсивно вычислить V(s1) и V(s2) и пересечь их: V(s) = V(s1)Ç V(s2). В конечном случае рекурсии (в наборе осталась только одна полуплоскость р) пересечение производить не надо, а необходимо просто возвратить эту полуплоскость в качестве результата на этом этапе V(ð).
При размере входного массива n, время работы программы t(n) определяется следующим рекуррентным соотношением:
(6)
В выражении (6) компонент an — это время, необходимое для формирования области пересечения двух выпуклых многоугольников. Соответствующие алгоритмы будут рассмотрены ниже. Таким образом, время, необходимое данному алгоритму для выполнения поставленной задачи, может быть оценено следующим образом:
. (7)
Известно, что для выполнения
задач подобного класса нижним временным пределом
является 
,
поэтому рассмотренный выше алгоритм можно
считать оптимальным.
Строя многоугольники Вороного для каждой точки из заданного набора точек F, мы получаем так называемые диаграммы Вороного (рис. 7). Очевидно, что диаграмма Вороного разбивает плоскость на выпуклые многоугольники, кроме того, конфигурации этих многоугольников полностью удовлетворяют поставленной перед нами задаче.
Предположим, что на плоскости задан некий многоугольник и точка. И пусть требуется определить, принадлежит ли точка многоугольнику. Определить принадлежность точки выпуклому многоугольнику значительно легче, чем произвольному, поэтому сначала рассмотрим именно этот случай.
Так как многоугольник выпуклый, то точка лежит вне этого многоугольника только в том случае, когда она окажется слева от какого-нибудь ребра, при последовательном обходе ребер многоугольника по часовой стрелке (рис. 8).
Следовательно, алгоритм будет состоять в последовательном обходе ребер многоугольника и анализе взаимного положения точки и ребра.
Этот анализ можно произвести,
исходя из следующих соображений (рис. 9). Точка
р3 находится слева от вектора 
тогда и только тогда, когда 
,
где 
,
а 
.
Точка р3 находится справа от вектора 
тогда
и только тогда, когда 
.
Проведем теперь к вектору 
перпендикуляр 
.
Вектор 
,
исходя из свойства (*) скалярного произведения:
.
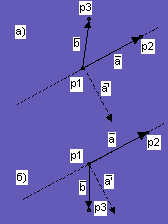
Теперь можно задать условие
взаимного положения вектора 
и точки р3 через угол 
:
точка р3 находится слева от вектора 
тогда и только тогда, когда 
,
а точка р3 находится справа от вектора
тогда и только тогда, когда 
.
Из определения скалярного произведения двух векторов следует, что
. (8)
Используя выражение (8) и свойство скалярного произведения (7), приходим к критерию определения взаимного положения вектора и точки:
Точка р3 находится относительно
:
(9)
Тот же результат можно получить, используя не скалярное, а векторное произведение.
Теперь, разобрав этот простой алгоритм, вернемся к общему случаю, то есть к определению взаимного положения точки и произвольного многоугольника.
Решим задачу о принадлежности точки произвольному многоугольнику методом луча. Предположим, что необходимо определить принадлежность точки a некоторому заданному многоугольнику (рис. 10). Для решения этой задачи проведем прямую из точки а в некоторую бесконечно удаленную от многоугольника точку. На всем своем протяжении эта прямая может n раз пересечь границу нашего многоугольника. Если прямая не пересекает ни одного ребра заданного многоугольника, то n=0. Если следовать по прямой из бесконечно удаленной точки к точке a, то первое пересечение приведет нас внутрь многоугольника, при втором пересечением мы выйдем за границу этого многоугольника, при третьем — снова окажемся внутри и т.д. Из этих наблюдений можно заключить, что каждое нечетное пересечение означает попадание внутрь нашего многоугольника, а каждое четное — выход из него. Таким образом, если при движении по прямой только что описанным образом, мы попадаем в точку a с нечетным числом пересечений границы многоугольника, то точка a находится внутри него, если же число пересечений четно, то точка лежит вне многоугольника. Применяя эти заключения к ситуации, отображенной на рис. 10, находим, что точка a лежит снаружи многоугольника, а точка b — внутри.
принадлежности точки произвольному многоугольнику
Можно сделать следующие упрощения. Во-первых, для простоты в качестве прямой можно взять луч, который параллелен одной из осей декартовой прямоугольной системы координат и проходит через точку a. Во-вторых, так как порядок пересечения луча с ребрами не важен, то можно просто последовательно перебирать ребра многоугольника, подсчитывая те ситуации, когда луч пересекает ребро, а затем просто определить четность числа пересечений.
Однако при таком подходе возможен ряд исключительных случаев (рис. 11). В случаях, описанных в пункте (а), происходит пересечение нескольких ребер, но мы будем рассматривать такие ситуации как однократные пересечения с границей многоугольника, то есть будем инвертировать четность числа пересечений. В случаях же, изображенных в пунктах (б) и (в) мы будем сохранять четность неизменной. На этом описание алгоритма определения принадлежности точки произвольному многоугольнику можно считать законченным.
При формулировке алгоритма построения многоугольников Вороного часто упоминается о необходимости пересечения двух выпуклых многоугольников (все многоугольники, получающиеся во время действия этого алгоритма, являются выпуклыми). Будем рассматривать задачу о вычислении области пересечения S двух выпуклых многоугольников N и M. Многоугольник S может получиться:
Многоугольник S в любом случае будет выпуклым, так как является областью пересечения выпуклых многоугольников (мы не будем здесь останавливаться на доказательстве этого факта). Для определения принадлежности одного выпуклого многоугольника другому, достаточно проверить принадлежность второму многоугольнику всех вершин первого. Поэтому первые три случая не представляют для нас сейчас интереса (несколько ранее были приведены алгоритмы определения принадлежности точки многоугольнику, которых достаточно для разрешения этих случаев). На четвертом же (самом важном и интересном) случае остановимся подробнее.
Итак, предположим, что два выпуклых многоугольника N и M пересекаются невырожденно, образуя при этом выпуклый же многоугольник S=NÇ M. Исходя из этого можно утверждать, что многоугольник S будет состоять из чередующихся цепочек вершин многоугольников N и M, причем каждые две соседние цепочки будут соединяться в соответствующей точке пересечения многоугольников N и M (рис. 12).
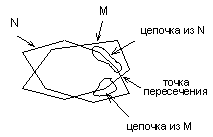
Известно несколько решений этой задачи. Для двух заданных на входе выпуклых N и M многоугольников алгоритм определяет по одному окну. Под окном мы будем понимать выделение текущей вершины многоугольника. В процессе работы алгоритма по мере формирования многоугольника пересечения происходит попеременное продвижение этих окон вдоль границ соответствующих многоугольников в направлении движения часовой стрелки. Это попеременное движение необходимо для последовательного поиска точек пересечения исходных многоугольников N и M. Отсюда видно, что обнаруживаемые точки пересечения следуют в том порядке, в котором они располагаются вокруг многоугольника S=NÇ M, поэтому об окончании формирования этого многоугольника можно говорить тогда и только тогда, когда первая из точек пересечения найдена вторично. В противном случае, если в продолжение некоторого необходимого числа итераций, равного 2*(|N|+|M|), не найдена ни одна точка пересечения, это будет означать, что многоугольники N и M не пересекаются (случай 1, 2 или 3).
Для дальнейшего детального объяснения работы алгоритма необходимо ввести понятие серпа. Под серпом будем понимать такой многоугольник, который ограничен цепочкой вершин из многоугольника N и цепочкой из многоугольника M, ограниченных двумя последовательными точками пересечения (рис. 13). Ту часть серпа, которая принадлежит многоугольнику пересечения, будем называть внутренней цепочкой серпа. Если на некотором участке границы многоугольников совпадут, то в этом случае будет образован вырожденный серп. Не принимая к рассмотрению случай полного совпадения исходных многоугольников (эту ситуацию отнесем к случаю 2 или 3), можно утверждать, что многоугольник пересечения будет окружен четным числом серпов, внутренние цепочки которых, то есть последовательные участки многоугольника пересечения, попеременно являются частями границ многоугольников N и M.
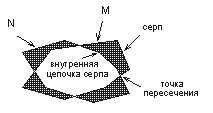
Алгоритм поиска многоугольника пересечения можно разделить на две фазы. Первая фаза представляет собой набор подготовительных операций, сводящихся к установке окон обоих многоугольников над вершинами, принадлежащими одному и тому же серпу. Для этого окно n многоугольника N и окно m многоугольника M перемещаются в направлении движения часовой стрелки до тех пор, пока они не будут установлены на ребрах (ребро у нас будет определяться своим началом), принадлежащих одновременно одному и тому же серпу. Оба окна начинают свое движение с произвольной позиции.
Во время второй фазы окна n и m продолжают свое движение, но теперь это движение строго упорядочено от одного серпа к соседнему серпу. Перед переходом одного из окон к следующему серпу происходит пересечение текущих ребер, то есть тех ребер, начальные точки которых находятся в окнах n и m, в точке, соединяющей текущий и соседний серп. Многоугольник пересечения строится именно во время этой фазы, которая является основной в алгоритме. Перед каждым перемещением окна (m или n) в многоугольник пересечения заносится конечная точка ребра, находящегося в данный момент в этом окне, в том и только в том случае, если это ребро принадлежит внутренней цепочке текущего серпа. При каждом пересечении ребер, находящихся в окнах n и m в многоугольник пересечения добавляется точка пересечения этих ребер.
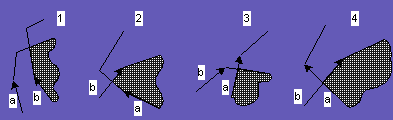
Очевидно, в процессе работы алгоритма на каждой его итерации будет возникать вопрос: какое из окон необходимо продвинуть на этом этапе, а какое нет. Ответ на этот вопрос даст следующее правило, которое основано на понятии нацеленности одного ребра на другое. Говорят, что ребро a нацелено на ребро b, если бесконечная прямая, определяемая ребром b, расположена перед a. Если ребра a и b коллинеарные, то ребро a нацелено на ребро b, если конечная точка ребра a не лежит после b. Это дополнение к определению будет использовано для того, чтобы продвинуть a вместо b, когда два ребра пересекаются вырожденно (то есть более чем в одной точке). Этим обеспечивается недопустимость пропуска ни одной точки пересечения.
Сформулируем теперь упомянутое выше правило перемещения. Оно дает возможность отличить текущее ребро, которое может содержать следующую точку пересечения, от текущего ребра, которое возможно не может содержать следующей точки пересечения. Нам необходимо различать четыре ситуации (рис. 14).
Осталось доказать следующее утверждение: если границы многоугольников N и M пересекаются, то текущие ребра (то есть ребра, находящиеся в окнах многоугольников) n и m пересекаются в некоторой точке после не более, чем 2(|N|+|M|) итераций алгоритма. Для доказательства предположим, что многоугольники N и M пересекаются. После |N|+|M| итераций либо n, либо m должны совершить полный оборот вокруг соответствующего многоугольника. Предположим, что это произошло с n. В одной из этих итераций ребро n должно быть расположено так, что ему будет принадлежать точка пересечения наших многоугольников. Таким образом, мы установили, что для достижения начальных позиций n и m потребуется не более |N|+|M| итераций. Реально, такая ситуация, либо аналогичная ей при взаимном изменении ролей n и m, будет достигнута за меньшее число итераций. Так как после этого ни n, ни m не будут продвинуты на полный оборот вокруг своих многоугольников, прежде чем будет достигнута первая точка пересечения, потребуется не более |N|+|M| дополнительных итераций. Отсюда и получается 2(|N|+|M|).
Знание этого алгоритма дает возможность весьма эффективно искать пересечение выпуклых многоугольников. Значительно сложнее задача о пересечении выпуклого многоугольника с произвольным. Сложность ее главным образом состоит в том, что в качестве ответа может выступать не единственный многоугольник, как это было раньше, а непредсказуемое число самостоятельных многоугольников. Еще сложнее задача пересечения двух произвольных многоугольников, которая здесь нами рассматриваться не будет. Мы рассмотрим лишь более гибкий (по отношению к уже рассмотренному алгоритму) инструмент решения задач о пересечении двух многоугольников — алгоритм Сазерленда-Ходжмана, который снимает ограничение о выпуклости одного из многоугольников.
Алгоритм Сазерленда-Ходжмана по заданному выпуклому отсекающему многоугольнику P и произвольному исходному многоугольнику Q формирует область PÇ Q, которая представляет собой в общем случае набор многоугольников, содержащий нуль или несколько членов-многоугольников.
Суть данного алгоритма состоит в поочередном выполнении отсечения произвольного многоугольника Q относительно каждого ребра выпуклого отсекающего многоугольника P. Исходный многоугольник Q сначала отсекается по первому ребру отсекающего многоугольника P, затем полученный многоугольник отсекается по второму ребру и так далее, пока не будут перебраны все ребра отсекающего многоугольника P. Когда исходный многоугольник будет отсечен по каждому из ребер отсекающего многоугольника, задача считается выполненной. На рис. 15 проиллюстрирована работа алгоритма, где в качестве отсекающего многоугольника для простоты взят прямоугольник.
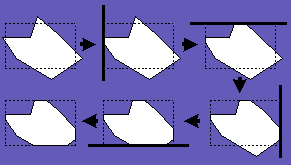
На каждой итерации алгоритма
происходит отсечение исходного многоугольника
по правой стороне ребра отсекающего многоугольника
(за направление обхода ребер в многоугольнике
принято направление движения часовой стрелки).
Непосредственно отсечение многоугольника
по ребру происходит следующим образом: в результате
попарного сравнения ребра отсекающего многоугольника
с каждым ребром 
исходного многоугольника, в создаваемый многоугольник
добавляются две, одна или ни одной вершины.
При сравнении каждой пары ребер возникнет одна из следующих четырех ситуаций (рис. 16):
полностью лежит справа от ребра 
.
В создаваемый многоугольник необходимо
добавить вершину b.
пересекает ребро 
справа налево. В создаваемый многоугольник
необходимо добавить точку, в которой пересекаются
эти ребра.
полностью лежит слева от ребра 
.
В создаваемый многоугольник добавлять
ничего не нужно.
пересекает ребро 
Если этому алгоритму необходимо будет обработать такой многоугольник, что после отсечения должны будут получиться несколько самостоятельных многоугольников, то алгоритм “возвратит” набор многоугольников. Так как по своей сути он возвращает только один многоугольник, то многоугольники возвращаемого набора будут связаны в один вырожденными ребрами (рис. 17).
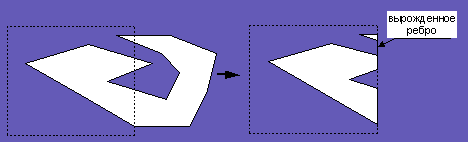
Если необходимо получить набор самостоятельных многоугольников, то после завершения работы алгоритма нужно будет просто преобразовать многоугольник, полученный с его помощью в множество (список или массив) самостоятельных многоугольников.
Данная статья является в какой-то мере обзорной, может быть даже вводной, для практического использования фундаментальных понятий аналитической геометрии. К сожалению, были рассмотрены только простейшие алгоритмы, далеко не всегда являющиеся самыми интересными. Существует, например, так называемый алгоритм Вейлера-Атертона — алгоритм отсечения многоугольников, который по справедливости можно назвать общим для многоугольников. Он позволяет обрабатывать любые исходные и отсекающие многоугольники, которые не обязательно должны быть выпуклыми и могут даже включать отверстия.
В статье была использована следующая литература: Ахо, 1979; Препарата, 1989; Ласло, 1997; Боресков, 1996.
