2. МЕТОДЫ АНАЛИЗА ЕЯ ОПИСАНИЯ ПРЕДМЕТНЫХ ОБЛАСТЕЙ

2.1. Количественная спецификация ЕЯ описания

Статистический анализ естественно-языкового описания

Применением аппарата математической статистики в исследовании ЕЯ представлений ПОРМ занимается раздел лингвистики “Лингвистическая статистика”. Согласно энциклопедии “Русский язык”7 , лингвистическая статистика — раздел языкознания, занимающийся статистическими методами количественных закономерностей в языке и речи. Первичным материалом в лингвистической статистике является текст, рассматриваемый как последовательность лингвистических единиц заданного уровня: букв или фонем, морфов или морфем, словоформ или лексем, словосочетаний, предложений. На этом материале изучаются количественные характеристики лингвистических форм — их употребительность, совместная встречаемость, законы распределения в тексте, их физические размеры. На основе полученных данных описываются свойства текста, формулируются гипотезы о механизмах его образования и об устройстве системы языка. Основные понятия и категории в лингвистической статистике заимствуются у математической статистики. Такими понятиями являются понятия генеральной совокупности и выборки, частоты и вероятности, вероятностные распределения и статистические оценки. Однако применение этих понятий к лингвистическому материалу имеет ряд особенностей. В частности, в языкознании могут быть рассмотрены два принципиально разных вида генеральной совокупности: либо совокупность текстов (корпус текстов) одинакового жанра, заданного списка авторов или заданного временного интервала, либо совокупность единиц, принадлежащих одному лингвистическому уровню: фонем, морфем, слов или предложений.

Лингвистическая статистика как научное направление возникла в связи со стремлением дополнить совокупность структурных характеристик лингвистических единиц характеристикой их употребительности. Это основано на предположении, что любая лингвистическая единица обладает априорно присущей ей вероятностью быть употребленной в тексте заданного класса. Основные понятия лингвистической статистики и методические указания по применению математических методов можно найти у К.Б.Бектаева и Р.Г.Пиотровского [Бектаев, 1974].

Модель “ранг-частота”

Модель “ранг-частота” связывает абсолютную частоту слова с его рангом (порядковым номером в частотном словнике, упорядоченном по убыванию частоты). Наиболее известны законы Ципфа и Мандельброта. Эти законы не являются статистическими, но характеризуют динамическую зависимость абсолютной частоты слова от его ранга.

Закон Ципфа

Исследования количественных параметров текстов проводятся достаточно давно. Наиболее известные результаты были получены Ж.-Б.Эступом (Jean Baptiste Estoup) и связаны с эмпирическим анализом использования слов в естественно-языковых текстах. Первым теоретическим результатом в области статистического анализа текста считается эмпирический закон, установленный Дж.К.Ципфом (George Kingsley Zipf), получивший название “закона частот слов”. Закон связывает гиперболической зависимостью частоту встречаемости слова в тексте с рангом этого слова в списке, упорядоченном по убыванию частот:

i(k, r) = pk r-b.

(1.0)

где i(k,r) — частота слова в тексте, k — общее число слов в тексте, r — ранг слова, т.е. его порядковый номер в упорядоченном по убыванию частотной функции словнике.

В первом приближении, именно это и установил Ципф, коэффициент p принимает значение 1/10 (=0.1).

В настоящее время не существует убедительного обоснования данного закона. Ципф объяснял свой закон как следствие общего принципа “наименьшего усилия” — наиболее часто встречающиеся слова любого языка обычно являются короткими служебными словами, употребление и восприятие которых требует наименьших усилий (чем и объясняется их большая частота) [Солтон,1979. С.186–187]. Вместе с тем в литературе приводится косвенное обоснования необходимости такой зависимости, т.е. осуществляется “вывод закона” исходя из различных предположений [Мандельброт,1973. С.330–336].

Анализ закона и его косвенных обоснований позволяет сделать вывод о том, что дело не в “наименьших усилиях”, а в существовании единых системных правил построения языкового описания, вернее использования субъектом метода формализации своих знаний на основе естественно-языкового описания.

Закон Мандельброта

Последующие исследования текстов в различных естественно-языковых системах (разных языках) не подтвердили точного выполнения соотношения (1.0) для найденных Ципфом коэффициентов. Не соответствует данному закону “поведение” наиболее часто употребляющихся слов, а также редких, которые характеризуют “богатство словарного состава” текста. Б.Мандельброт (Benoit Mandelbrot) предложил иную формулу для описания “закона частот слов”, в которой были учтены названные несоответствия:

i(k,r) = pk (r+v)-b.

(1.1)

Общий вид зависимостей (1.0) и (1.1) представлен на рис. 1

Получим выражения для приближенной оценки параметров закона Мандельброта.

Для этого выполним следующие преобразования:

, где — относительная частота встречаемости слова.

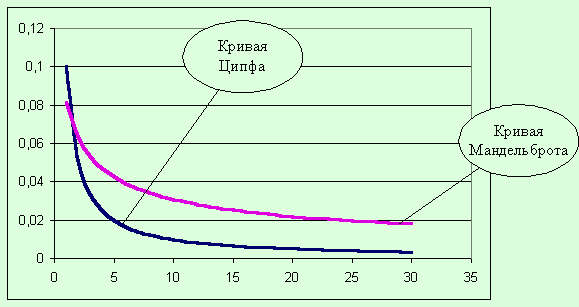
Рис. 1. Вид зависимостей Ципфа и Мандельброта

Таким образом, имеем

, где .

(1.2)

Представим формулу (1.2) в виде степенного многочлена Тейлора:

....

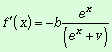
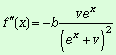
Если коэффициенты в многочлене Тейлора обозначить через С0,C1,...,Cn, то будем иметь

....

Откуда имеем приближенные выражения для параметров через коэффициенты:

.

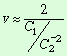
Получим коэффициенты степенного ряда методом наименьших квадратов по имеющимся значениям частотной функции.

Имеем S(T) = (<w, N(w,T)>). Будем исследовать следующие величины:

, где — относительная частота слова w в тексте T.

Введем обозначения:

Будем искать аппроксимирующую функцию в виде многочлена:

, для этого необходимо минимизировать следующую функцию:

.

Вычислим частные производные этой функции и приравняем их к 0.

....

Получаем систему линейный уравнений относительно С0,..,Cn:

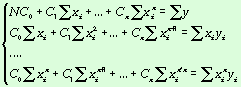
Решая эту систему (например, методом Гаусса [Ракитин, 1998]), можно получить вектор коэффициентов C0,...,Cn.

Используя полученные значения, можно вычислить коэффициенты закона Мандельброта. Полученные формулы дают приближенные значения параметров закона Мандельброта и позволяют описать характер изменения частот слов для малых значений ранга.

Более точные значения оценок параметров могут быть получены для закона Ципфа. В этом случае имеет место линейная зависимость логарифма относительно частоты слова от логарифма его ранга:

.

Используя метод наименьших квадратов, также можно найти значения коэффициентов для прямой:

 

Получение статистического закона распределения слов в модели “ранг-частота”

Используя предложенную Мандельбротом зависимость, попробуем получить статистический закон распределения слов по частоте:

.

Во-первых, необходимо, чтобы закон удовлетворял условию нормировки, а именно требуется выполнение равенства:

.

Вычислим интеграл и найдем нормировочное выражение:

.

Таким образом, закон распределения слов по частоте можно записать в виде

.

(1.3)

Вычислим основные характеристики распределения: математическое ожидание и дисперсию.

По определению математического ожидания имеем

.

Вычислим начальный момент второго порядка:

Воспользуемся формулой для вычисления дисперсии:

Итак, в результате имеем выражения для математического ожидания и дисперсии:

 

(1.4)

Используя метод моментов, легко получить значения параметров статистического распределения (1.3). Из формул (1.4) имеем

.

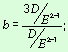
Здесь E и D — математическое ожидание и дисперсия в генеральной совокупности.

Спецификация ЕЯ описания ПОРМ это не только выявление основных соотношений в его лексическом составе, но и соотнесение его с другим описаниями. Выделение конкретной предметной области из их множества или разделение всего естественно-языкового описания на некоторые частичные подобласти, соответствующие подобластям ПОРМ, также является задачей спецификации. Фактически спецификация ЕЯ описания ПОРМ сводится к задаче формирования корпуса текстов, релевантных по отношению к изучаемой предметной области. Формальное решение данной задачи может быть получено различными методами. К числу наиболее известных решений относятся решения на основе “закона рассеяния Бредфорда”.

Закон Бредфорда

Вопросами спецификации естественно-языковых описаний в печатной (полиграфической) форме занимается библиометрия. С. Бредфорд (S.C.Bradford), занимаясь исследованиями в данной отрасли знаний и деятельности, установил эмпирическую закономерность, связывающую количество журналов и количество опубликованных в них статей на ту или иную тему. Он сформулировал это так: “Если научные журналы расположить в порядке убывания числа содержащихся в них статей по какому-нибудь предмету, в полученном списке можно будет выделить ядро, состоящее из журналов, непосредственно посвященных этому предмету , и несколько групп зон, содержащих такое же количество публикаций, как в ядре, причем журналы в ядре и в последовательно расположенных зонах составляют отношение 1 : n : n2 : ...” [Солтон, 1979. С.187–188].

В дальнейшем этот вывод получил развитие и его можно представить следующим уравнением. Пусть J названий журналов на данную тему разбиты на k групп, каждая из которых содержит по J1, J2, ..., Jk названий, так что все группы содержат одинаковое количество статей на данную тему; тогда

(1.5)

где i = 1, 2, ..., k; k = 1, 2, ..., m; J1 — количество журналов в ядре; bk > 1 — так называемый множитель Бредфорда для разбиения J названий на k групп.

В терминологии, используемой в данной работе, эти соотношения можно трактовать как связь между интенсивностью интеллектуальной деятельности людей по формализации своих знаний (авторов печатных изданий), измеряемую количеством ЕЯ описаний ПОРМ (опубликованных статей), с количеством подобластей ПОРМ (журналов), на которые разделяется всё естественно-языковое описание.

Из формулы (1.5) следует, что для любой совокупности статей G существует такое максимально возможное количество зон m, что все области содержат одинаковое количество текстов. Для этого максимума m значения Ji=J и bm минимальны, а J1 — наименьшее возможное ядро, состоящее из наиболее “продуктивных” подобластей.

В [Солтон, 1979] приводится вывод основных параметров “бредфордова ядра”, т.е. той области, которая содержит основу тематических знаний, релевантный набор текстов.

Формирование ядра релевантных текстов может быть построено на методе, суть которого сводится к использованию некоторого статистического критерия согласия для сравнения количественных спецификаций текстов. В конкретном случае можно сравнить частотные словники текстов. Главной идеей, лежащей в основе этого подхода, является гипотеза о том, что в текстах, “принадлежащих” одной предметной области, значения частотных функций слов приблизительно совпадают. Иными словами, эмпирические функции распределения слов по частоте близки друг другу.

В общем случае для сравнения двух упорядоченных последовательностей значений частотной функции текстов T1 и Т2 могут использоваться различные коэффициенты корреляции, например: Пирсона (E.S.Pearson), Спирмена (C.Spearman), Кендалла (M.G.Kendall), дихотомический (в случае преобразования ранговых шкал) [Гласс,1976. С.142–165]. Могут использоваться при соответствующих преобразованиях и статистики для проверки значимости разностей пар [Закс,1976. С.286–287]. Для сравнения эмпирических частотных функций распределения можно использовать критерий согласия Вилкоксона (F.Wilcoxon) [Закс,1976. С.288; Гмурман, 1998], в котором не требуется знание ни функции распределения, ни каких-либо параметров распределения.

В качестве примера [Прохоров, 1999] рассмотрим использование критерия Вилкоксона для проверки однородности двух независимых выборок. Под выборкой будем понимать совокупности исследуемых ЕЯ-единиц, т.е. слов, которые принадлежат некоторому тексту, входящему в корпус текстов G. Другими словами, выборкой из генеральной совокупности G будет являться один из его элементов, т.е. текст. Поскольку задачей и является правомерность внесения текста в генеральную совокупность, то выборкой может являться в принципе любой текст, но в генеральную совокупность попадут только те, для которых функции распределения слов по частоте будут одинаковы.

Построим алгоритм определения однородности двух текстов, а затем опишем процесс формирования ядра.

Пусть имеются два текста T1 и Т2, для которых построены частотные словники S(T1) и S(T2). На основании словников построим два упорядоченных множества слов:

S1 = ( w11, w12, w13,...,w1N )

S2 = ( w21, w22, w23,...,w2M )

Порядок, в котором расположены слова, зависит от значения их частотных функций и противоположен порядку в соответствующих частотных словниках. Пронумеруем все элементы множества S1: S1 = (1,2,3,4,5,6...N), а затем, используя числа для нумерации слов в S1, пронумеруем элементы множества S2. Словам, которые встречались в S1, присваиваются номера из S1, всем остальным словам присваиваются порядковые значения: меньшие номера, словам с меньшей частотой. Так, S2 может иметь следующий вид: S2 = (1,3,2,5,N,4, N+1,N+2,...). Чтобы исключить совпадения в S1 и S2, ко всем их элементам добавляется относительная частота встречаемости слов, для слов словников S(T1) и S(T2) соответственно. Относительная частота <1, поэтому она не может повлиять на соотношения между элементами множеств S1 и S2.

Полученные значения являются исходными данными для их использования в критерии согласия Вилкоксона. Объединим теперь оба множества в одно, расположив элементы в порядке возрастания, пронумеруем их и просуммируем индексы тех элементов, которые принадлежат S1. Полученное число обозначим как Wнабл.

Будем считать, что размеры обоих выборок (N и M) больше 25. Тогда при справедливости гипотезы об однородности выборок и заданном уровне доверия должно выполняться неравенство:

,

где

,

Q — половина уровня доверия = a/2; zкр находится по таблице функции Лапласа по равенству

  .

В зависимости от способа применения изложенного метода можно получать различные формы ядра ЕЯ описания ПОРМ, поскольку метод предполагает наличие минимум двух текстов. Можно рассмотреть некоторые варианты:

Построение ядра ЕЯ описания ПО на основе эталонного текста. Этот способ предполагает наличие эталонного текста, для которого установлена его релевантность к изучаемой предметной области (в случае, если текст является одним из выпусков журнала, то сделать это можно, например, по заголовку). Затем выполняется проверка гипотезы об однородности текстов для каких-либо еще текстов и принимается решение о включении или не включении текста в исследуемый корпус текстов. Условно эту методику можно изобразить в виде звезды (рис. 2):

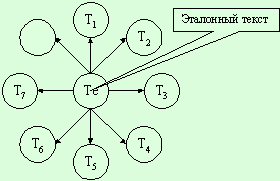
Рис. 2. Звездообразная топология ядра ЕЯ описания ПО

Линейная схема построения ядра ЕЯ описания ПО. Суть этого подхода в том, что в нем нет заранее определенного эталонного текста. Эталонный текст существует только на время сравнения. После принятия гипотезы об однородности роль эталонного текста начинает выполнять новый включенный в корпус текст. Графически этот процесс можно представит в следующем виде:

Рис. 3. Линейная топология ядра ЕЯ описания ПО

Результат такого метода может оказаться сомнительным, во всяком случае когда исходный (начальный текст) оказался недостаточно релевантным или вовсе нерелевантным ПОРМ.

Данный метод может быть реализован и путем накопления частот, т.е. использования в качестве характеристик эталонного текста результата сложения частотных словников.

Полносвязная схема построения ядра ЕЯ описания ПО. В полносвязной схеме также не существует выделенного эталонного текста. Но в отличие от линейной схемы для включения некоторого текста в корпус необходимо подтверждения гипотез однородности от всех имеющихся к данному моменту в ядре текстов. Иными словами, чтобы включить в корпус новый текст, необходимо подтвердить гипотезу об однородности между ним и всеми текстами, уже включенными в корпус. Графически это выглядит следующим образом:

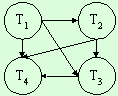
Рис. 4. Полносвязная сетевая структура ядра ЕЯ описания ПО

В самом общем случае способ построения ядра может оказаться более сложной процедурой и представлять собой реализацию задачи кластерного анализа. Как и в классической постановке задачи кластеризации, здесь будут стоять два вопроса: выбор центра (центров) кластеризации и определения границ кластеров.

2.2. Логико-статистические методы извлечения знаний

Дистрибутивно-статистический метод

Дистрибутивно-статический метод позволяет на основе частотной информации о ЕЯ единицах получать по некоторой заданной формуле количественную характеристику их связанности. Философия данного метода состоит в том, “что семантическую классификацию значимых элементов языка можно с большим основанием индуктивно извлечь из анализа текста, чем получить ее с некоторой точки зрения, внешней по отношению к структуре языка. Следует ожидать, что такая классификация даст более надежные ответы на проблемы синонимии и выражения смысла, чем существующие тезаурусы и списки синонимов, основанные главным образом на интуитивных ощущаемых сходствах без адекватной эмпирической проверки” [Москович,1971. С.115–116]. В основе всех вариантов метода лежат количественные оценки, которые характеризуют совместную встречаемость языковых единиц текста в контекстах определенной величины. Основная гипотеза метода состоит в том, что слова, встречающиеся вместе в пределах некоторого текстового интервала, как-то связаны между собой. Для оценки связанности вводится коэффициент “силы связи”, который рассчитывается по некоторой формуле. Вне зависимости от вида формулы в ней обычно используются характеристики совместной встречаемости пар слов и одиночной встречаемости каждого из слов. Обозначим их через NAB, NA и NB соответственно. Обычно через эти параметры и выражается искомая характеристика связанности слов.

Применение дистрибутивно-статистического метода связано с использованием понятия контекста. Любой текст можно представить как сумму непересекающихся контекстов:

Указанные характеристики NAB, NA и NB указывают не сами частоты слов A и B, а число контекстов, в которых наблюдалась совместная встречаемость (NAB), встречаемость только A (NA) и встречаемость только B (NB).

Приведем несколько формул, по которым часто производится расчет “силы связи” в дистрибутивно-статистическом методе [Москович,1971]:

 где

 — Т.Танимото (T.T.Tanimoto), Л.Дойл (L.B.Doyle).

 — М.Мэйрон (M.E.Maron), Дж.Кунс (J.Kuhns).

 — А.Я.Шайкевич, Дж.Солтон (G.Salton), Р.Куртис (R.M.Curtice).

.

Количественная характеристика, используемая для вычисления “плотных групп” (clumps ... — в дословном переводе с англ. “плотные группы”) [Needham, 1964; Dale, 1965]:

 — С.Деннис (S.Dennis).

В качестве оценки степени близости слов использовался так называемый “ассоциативный фактор”, который рассчитывается по формуле [Styles, 1963]:

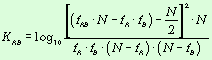 — Х.Е. Стайлз (H.E.Styles).

Все вышеприведенные критерии объединяет рассмотрение событий, связанных с появлением слов A и B как системы случайных явлений. А в качестве критерия, определяющего меру связи, используется следующий факт: если A и B — независимые события, то P(AB)=P(A)P(B).

Однако такой подход позволяет определить только степень независимости событий, а не величину динамической (функциональной) связи. Все формулы, какими бы расчетами они не были получены, требуют интерпретации. Та ассоциация, которую они извлекают из текста, требует дальнейшего анализа. Важным является выяснение, насколько полученные формально значения связей соответствуют ожидаемым, или возможным, объяснениям.

Величина контекста, в рамках которого осуществляются подсчеты коэффициентов “силы связи”, как показывают результаты исследований, позволяет наиболее вероятно устанавливать: а) при малых размерах контекста, ограниченного одним или двумя соседними словами — контактные синтагматические связи словосочетаний; б) при размере 5–10 слов — дистантные синтагматические связи и парадигматические отношения; в) дальнейшее увеличение ширины контекста до 50–100 слов (размер предложения, сверхфразового единства, абзаца) — тематические связи между словами. Тематические связи могут оказаться доминирующими, если принять размер контекста величиной с сам текст [Москович, 1971. С.120].

В результате вычислений на всем массиве текста формируется матрица связности слов (языковых единиц) или ассоциативная матрица, внешний вид которой представлен на рисунке рис. 5:

 

слово

...

ai

...

слово

частота

 

fa

 

 

 

 

...

 

bj

fb

...

fab

...

 

 

 

...

 

Рис. 5. Матрица ассоциативных связей

Дистрибутивно-статистический метод может использоваться как процедура формирования ядра тематически связанных между собой текстов. Кроме этого данный метод может использоваться и как технология автоматического составления тезауруса и, как следствие этого, в качестве формально-языковой системы для информационного поиска и индексирования.

Обобщенная методика разработки тезауруса на основе дистрибутивно-статистического метода выглядит следующим образом:

·         Составление частотных словников и конкордансов.

·         Анализ совместной встречаемости слов (языковых единиц) и составление на его основе матрицы ассоциативных связей.

·         Субъектная интерпретация матрицы ассоциативных связей и формирование классов типовых связей (отношений).

·         Группировка (выделение) отдельных типов отношений (родовидовых, каузальных и др.).

·         Интерпретация отдельных связей слов.

·         Группировка семантических полей.

Компонентный анализ

Метод компонентного анализа позволяет установить связь между двумя понятиями на основе анализа их дефиниций. Для реализации метода необходимым является наличие словаря определений. Возможны несколько основных модификаций данного метода. Рассмотрим эти варианты.

Количественная связь. В этом варианте два слова А и В считаются связанными силой связи fab = k, если в дефиниции каждого из них есть k общих слов — ,

Данный вариант компонентного метода позволяет построить множество тезаурусов различной степени связности. В общей системе потенциально связанных между собой слов можно выделить подмножество слов, связанных между собой силой связи f = k , k = =1, 2, 3, ..., K. Данное подмножество можно рассматривать как некоторый кластер. Фактически компонентный метод — это двухэтапный дистрибутивно-статистический анализ, на первом этапе которого осуществляется анализ связанности слов с помощью дополнительного средства парадигматического конструктива словаря определений.

Гипертекстовая ссылка

В данном варианте два слова А и В считаются связанными, если в дефиниции каждого из них есть хотя бы одно общее слово — xab., т.е. k = 1.

Кроме того, что это слово связывает слова А и В, оно еще является “отсылочным”, по нему возможен “переход” от слова А к слову В и обратно. Следует заметить, что этот вариант достаточно активно используется в лексикографических системах (электронных словарях и энциклопедиях), текстовых редакторах, информационно-справочных системах и т.д. Несмотря на практическую распространенность, работ, посвященных количественному анализу использования данного метода и применению его для анализа знаний, представленных в естественно-языковой и лексикографической формах, сравнительно мало.

Данный метод может использоваться для анализа системы определений, или словаря определений. Можно оценить качество словарных статей по числу их связей с другими словарными статьями, или по длине цепочки, которая образуется при попытке понять то или иное слово. Потенциально цепочка не может быть неограниченной, кроме этого ее длина прерывается субъектом в тех случаях когда он достигает понимания определения.

Возможны исследования и эксцерпций в словарях определений, а также словарей текстов, которыми фактически являются help-системы.

Частотно-семантический метод

Метод частотно-семантического анализа (ЧСА) является развитием метода компонентного анализа. Существо метода состоит в использовании в качестве критерия оценки семантической “силы связи” между словами одновременно двух характеристик дефиниций этих слов: общности дефинирующих элементов и частоты их встречаемости. Метод предложен Ю.Н.Карауловым и на его основе построен первый компьютерный семантический словарь русского языка [РСС,1982]. Словарь содержит 1600 понятий и 9000 слов, создан в 1980 г. и издан в 1982 г.

Исходными данными для ЧСА являлись: некоторые идеографические словари — они использовались для составления списка дескрипторов, краткий толковый словарь русского языка для иностранцев — для составления списка слов, толковые словари С.И. Ожегова и Д.Н.Ушакова — для установки дефиниций слов и дескрипторов.

В основе метода ЧСА лежит идея о целостности (интегрированности) ПОРМ и отражении этого в ООРМ и, в частности, в языке. Образное представление этой идеи выражается следующей цитатой: “... представьте себе силы семантического притяжения в виде повсеместно существующего, разлитого в языке поля, в которое помещены тела — лексические единицы языка. Разные единицы в этом поле взаимодействуют между собой так же, как атомы, молекулы, макротела, планеты и космические объекты — и на одном уровне, т.е. с однородными единицами, и межуровнево”. [Караулов,1981].

В рамках поставленного эксперимента по отработке данных методом ЧСА практическая задача состояла в том, чтобы распределить 9000 слов по 1600 дескрипторам, т.е. сформировать так называемые семантические поля (ареалы).

Формально отнесение слова к дескриптору (включение его в семантическое поле дескриптора) можно представить следующим образом:

если , то ,

где — значение силы семантической связи между словом wi и дескриптором dj; — множество допустимых значений силы семантической связи дескрипторов и слов; Dj = {wij} — множество слов дескриптора; wi — слово, i = 1...|W|, W = {wi} — множество слов; dj — дескриптор, j = 1...|D|, D = {dj} — множество дескрипторов.

Первый вопрос практического решения задачи построения семантических полей состоит в установлении способа сравнения слов. В среднем каждое слово и дескриптор имеют дефиницию, состоящую из 10 слов, т.е. в случае эксперимента это составляет ~110000 словоформ. Для сравнимости слов было введено понятие семантического множителя — элементарной единицы содержательного плана. Это понятие объединяет ряд других, ранее вводимых понятий: семантические компоненты, дифференциальные семантические признаки, семы, семантические маркеры, семантические классификаторы, лексические функции, элементарные значения и т.д. Основные предположения при этом введении состоят в следующем: а) семантическое пространство языка дискретно; б) набор элементов пространства конечен и обозрим; в) число комбинаций практически бесконечно; г) семантическое пространство элементарно, т.е. состоит из неразложимых элементов; д) семантические элементы одноплановы, т.е относятся к содержанию (являются единицами познания и мышления); е) семантические элементы образуют универсальный набор, т.е. носят общесубъектный характер и их число и набор одинаковы для различных языков.

Способы получения (означивания) семантического множителя. Семантические множители, которые используются для дефинирования других слов, являются полнозначными словами и представлены в различных словарных формах. Попытка формального сравнения словарных дефиниций вызывает явные сложности. Необходима предварительная процедура приведения форм семантического множителя к одной, или кодирования их неким единым знаком. Возможны несколько вариантов получения приведенной формы семантического множителя [Караулов, 1980]:

Лемматизация — получение канонической формы слова, т.е. сведение словоизменительных форм слова к исходной (для существительных — именительный падеж, единственное число; для прилагательных — именительный падеж, единственное число, мужской род; для глаголов — инфинитив и т.д.).Фактически при лемматизации все слова разбиваются на грамматические классы.

Свертка — свертывание слова, т.е. удаление гласных, кроме гласной первого слога, на основании статистической закономерности русского языка — наибольшей информативности согласных.

Выделение корня — представление слова корневой морфемой.

Выделение основы слова — представление слова несколькими морфемами, например префиксом (приставкой) и корнем.

Выделение квазиосновы слова — произвольной начальной части слова на основании факта сдвига смысла слова (его содержания) к его началу.

Методика получения семантического кода слова состоит в такой последовательности процедур:

Внесение самого кодируемого слова в его код.

Исключение повторений семантического множителя.

Фильтрация (удаление “нулевых” семантических множителей (например, явление, совокупность, система, и т.п.), грамматических слов (например, повести, поискать, придержать и т.п.), предлогов, союзов и т.п.)

Формирование квазиоснов слов.

Дополнительные процедуры, например лексикализация устойчивых словосочетаний: железная дорога — желдор.

После реализации методики получаются дескрипторные и словные множества семантических множителей, сопоставленные соответствующим дескрипторам и словам:

а) дескрипторные множества — ;

б) словные множества — .

Второй вопрос практического решения задачи построения семантических полей состоит в установлении частотных параметров семантических множителей. Каждому множителю x ставятся в соответствие две частотные характеристики и — частоты встречаемости в дефинициях дескрипторов и слов соответственно.

  где в числителе формул количество слов (дескрипторов), в которых встретился множитель x, а в знаменателе общее количество слов (дескрипторов).

Методика частотного анализа семантических множителей состоит из двух пунктов: а) вычисление частот и ; б) ранжирование и упорядочение множителей в дефинициях по возрастанию их ранга.

Третий вопрос практического решения задачи построения семантических полей состоит в определении критерия семантической связи слов и дескрипторов.

Разработка критерия связанности состоит из трех этапов: на первом этапе разрабатывается феноменологическая модель единичной связанности, на втором — связанности степени K, на третьем — степени связанности K с учетом частотных свойств семантических множителей.

Феноменологическая модель единичной связанности состоит в том, что если есть хотя бы один общий семантический множитель в дефинициях слов и дескрипторов, то они считаются связанными:

Феноменологическая модель связанности K состоит в том, что если есть K общих семантических множителей в дефинициях слов и дескрипторов, то они считаются связанными:

Модель связанности с учетом частот множителей (селективный критерий Караулова) для конкретного случая исследования была определена для степени связанности K і 2 и пороговой частоты семантического множителя на множестве дескрипторов . Таким образом получаем, что слово и дескриптор семантически связаны друг с другом, если их дефиниции содержат более двух одинаковых семантических множителя или если их дефиниции содержат хотя бы один общий семантический множитель и его частота на множестве дескрипторов больше шести, т.е.

если

то

Метод построения семантических полей состоит из следующих процедур: построение поля по феноменологической модели единичной связанности; сужение поля за счет учета числа совпадающих множителей; сужение поля за счет учета частоты семантических множителей.

Данный метод является весьма продуктивным, и на его основе могут быть построены более сложные методики. Его развитие состоит в поиске и применении более сложного селективного критерия, а также их некоторого множества.

Одним из направлений развития метода может быть нахождение более эффективных процедур получения семантического кода слова [Прохоров, 1999], при этом следует различать эффективность с точки зрения быстрого получения кода слова (квазиосновы) и эффективность последующего построения семантических полей.

2.3. Синтагматическая модель текста

Формальное описание основных синтагм

Для построения алгоритмов и программ, выполняющих статистический анализ, необходимо задать правила работы с ЕЯ единицами различных уровней [Филиппович, 1990а]. Конструктивными единицами отдельных уровней, непосредственно связанными с анализом естественно-языковых текстов, являются: корпус текстов, текст, контекст, сверхфразовое единство, предложение, словосочетание, слово, морфема, квазиморфема, слог, символ алфавита (буква). Анализ текста может осуществляться как на отдельном языковом уровне, так и на нескольких. Глубина анализа определяется количеством уровней, единицы которых в нем участвуют. Обобщим названные языковые единицы понятием синтагма, под которым в пределах данной работы будем понимать непроизвольную цепочку языковых единиц нижнего уровня (символов). Синтагмы каждого верхнего уровня состоят из синтагм нижних уровней. Выделим основные синтагмы наших построений: символ, слово, предложение, текст. Производными синтагмами будут являться: морфема, квазиморфема, слог, словосочетание, сверхфразовое единство, контекст и корпус текстов. Подобное деление позволяет, во-первых, построить формальное описание текста на основе теории формальных языков нечувствительно к морфологическим, синтаксическим и семантическим аномалиям ЕЯ представления ПОРМ; во-вторых, осуществлять обработку текстов ЕЯ описания ПОРМ, содержащих произвольный набор символов. Фактически это является выделением в отдельный блок комплекса задач так называемого предварительного анализа текста (структурного анализа, предредактора), являющегося предшественником блоков морфологического, синтаксического, семантического и прагматического анализа [Филиппович, 1990а].

Статистические методы анализа позволяют выявить синтагматическую структуру текста, под которой будем понимать комплекс синтагматических конструктивов, построенных на основе основных и производных синтагм. Основными синтагматическими конструктивами являются: тексты, различные словники (частичные и полные, прямые и обратные, частотные) и словоуказатели. В самом общем случае словник представляет собой упорядоченный список синтагм, а словоуказатель — индекс упорядоченного списка синтагм нижнего уровня по синтагмам верхнего уровня, а также по организационным единицам (том, часть, глава, страница, строка и т.д.).

В качестве примера построим формальные модели для следующих синтагм и синтагматических конструктивов: символа, слова, словосочетания, предложения, контекста, текста, корпуса текстов, частотного словника.

Алфавитом естественно-языкового описания предметной области будем называть множество AB, такое, что:

, где ABx — алфавиты современных естественных языков (различаются множества прописных и строчных букв), ABD — множество цифр, ABS — множество специальных символов, которые могут выступать в качестве букв слов:

.

Стоп-знак слова — элемент множества знаков, которые позволяют отделять в тексте слова друг от друга. Стоп-знак stW слова W является элементом транзитивного замыкания множества стоп-знаков:

 где

Как видно из определения, каждому слову ставится в соответствие некоторая цепочка стоп-знаков.

Словом в ЕЯ описании ПО будем называть конкатенацию элемента транзитивного замыкания множества AB и стоп-знака: .

Предложение будем рассматривать как конкатенация элемента транзитивного замыкание слов и их разделителей и стоп-знака предложения , где

Текст определяется аналогично предложению как конкатенация элемента транзитивного замыкания слов и их разделителей и стоп-знака текста: .

Определим контекстно-свободные грамматики (КС-грамматика), которые порождает ЕЯ описание ПО. Введем обозначения:

GT — грамматика, порождающая текст.

GS — грамматика, порождающая предложение.

GW — грамматика, порождающая слово.

N — множество нетерминальных символов.

T = AB U STW — множество терминальных символов.

S — начальный нетерминальный символ.

EOF = <конец_файла>.

EOL = (<переход_на_след_строку> <возврат_каретки>)2.

Описание грамматики, порождающей текст.

GT = (N, T, P, S0)

N = { S0,S1,S2,S3,S4}

T = AB U STW

 

 

 

 

 

 

 

 

 

Описание грамматики, порождающей предложения.

GS = (N, T, P, S0)

N = { S0,S1,S2,S3,S4}

T = AB U STW

 

 

 

 

 

 

 

 

Описание грамматики, порождающей слова.

GW = (N, T, P, S0)

N = { S0,S1,S2,S3 }

T = AB U STW

 

 

 

 

 

 

Из сравнения грамматик GT и GW следует, что грамматика GT может порождать в том числе и отдельные слова, т.е. любое w, выводимое из GW, выводимо также из GT. Иными словами, , где Т — текст, w — отдельное слово.

Приведенные грамматики основных синтагм позволяют построить алгоритмы их извлечения из ЕЯ описания ПОРМ и вычислить все необходимые количественные атрибуты. Статистические методы обработки ЕЯ информации будут оперировать с формальными объектами, в частности, со словами и предложениями.

Формальное описание производных синтагм и синтагматических конструктивов

Одним из основных понятий статистических методов анализа является понятие генеральной совокупности. В качестве генеральной совокупности будем рассматривать корпус текстов ЕЯ описания ПОРМ, подлежащий исследованию. Объектом исследования являются отдельные синтагмы, являющиеся элементами этого корпуса текстов. Их основной и первичной характеристикой будет являться абсолютная частота встречаемости синтагмы в тексте (или корпусе текстов). Будем различать абсолютные частоты синтагм как для всего корпуса текстов, так и для отдельных его составляющих. Приведем формальное описание производных синтагм и синтагматических конструктивов:

Корпус текстов G — это множество текстов ЕЯ описания ПОРМ:

G = { T1, T2, ..., TN }, где N — число текстов в корпусе, Ti — i-й текст.

Словосочетанием будем называть wk , которое выводится из GT., состоящее ровно из k-слов, между которыми отсутствуют стоп-знаки предложения или текста (разделители между словами, всегда присутствующие в тексте, будут подразумеваться, но не записываться):

wk = w1w2w3..wk.

Очевидно, что любое отдельное слово w = w1.

Поставим в соответствие каждому выражению wk число, характеризующее частоту его встречаемости в конкретном выводе GT (т.е. в конкретном тексте). Таким образом, имеем отображение: , здесь E — множество целых чисел. Это отображение будем называть частотной функцией и будем обозначать:

N(wk, T), где T — конкретный текст, а wk — словосочетание.

Очевидно, что , если , и , если . Из w = w1 следует, что N(w,T) = N(w1,T).

Пусть T1 и Т2 — тексты, выводимые из GT. Тогда будем называть суммой текстов T1 и Т2 объект Т3, который будет получаться удалением из текста T1 стоп-знаков текста и обычным присоединением текста T2 к тексту T1. Можно доказать, что T3 — тоже является текстом, выводимым из GT, Если существуют T1 и T2, выводимые из GT, то существует конкретный вывод T1 и T2 из аксиомы S0. Очевидно, что T1 и Т2 — это конечные последовательности символов терминального алфавита GT, а сама грамматика может порождать последовательности любой длины (вследствие леммы о разрастании КС-языков). Следовательно, после вывода всех символов T1 можно осуществить вывод дополнительно всех символов T2. Таким образом, T3 есть текст, также порождаемый GT. Будем записывать: T3 = T1 + T2. Очевидно, что , т.е. сложение текстов не коммутативно.

Введем понятие контекста С(T). Контекстом в тексте T будем называть непрерывный фрагмент текста T, т.е. фрагмент вывода в GT. Контекст также можно считать текстом и ввести для него аналогичные операции. Свойствами контекста являются:

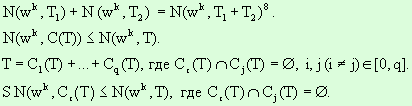
Введем понятие частотного словника. Частотным словником текста T будем называть упорядоченную совокупность следующих пар: слов (или словосочетаний) текста и значений их частотной функции.

S(T) = ( <wk, N(wk,T)>).

Как правило, частотный словник упорядочен по убыванию частотного признака. Частотный словник является основным объектом, который несет информацию о частотных характеристиках изучаемых языковых единиц.

Введем операции над словниками:

Объединение словников. Объединением словников S(T1) и S(T2) будем называть словник S(T1+T2). В объединенный словник войдут все слова и словосочетания из обоих текстов со своими частотными функциями, а для одинаковых слов (или словосочетаний) строится суммарная частотная функция (см. свойство (2.2)).

Вычитание словников. Вычитанием словников S(T1)–S(T2) будем называть словник S(T*), в который войдут только те слова (или словосочетания) из T1, для которых N(wk,T1) > N(wk,T2). Под T* понимается гипотетический текст, по которому мог бы быть построен словник S(T*).

Представленный пример является формальным описанием или синтагматической моделью естественно-языкового описания ПОРМ. Данная модель является порождающей. В зависимости от примененных формальных грамматик и теоретико-множественных определений в самом общем случае возможно множество различных синтагматических структур. Вполне понятно, что полученные таким образом синтагматические описания могут отражать ту или иную специфику исследования и обладать некоторыми ограничениями. Так, в рассматриваемом примере ограничениями являются: невозможность различения в словах дефиса, фактическое распознавание только двух синтагм (слова и предложения), невозможность распознавания вложенных структур (скобочных записей, прямой речи, других формально-синтаксических конструкций). По каждой порождающей синтагматической структуре возможно построение распознающей модели и реализация ее в виде “программ-трансляторов”. Генерирующая часть этих программ формирует синтагматический код естественно-языкового описания ПОРМ в виде комплекса конструктивов — словников и словоуказателей.

Приведенный пример позволяет говорить о преобразовании корпуса текстов G в частотный словник слов S(T). Однако потенциально описанная порождающая модель может использоваться для получения других синтагматических конструктивов: списков словосочетаний, контекстов, различных индексов и т.п.

В общем случае можно сформулировать следующее определение:

синтагматической моделью текста является представление его в виде множества основных синтагматических конструктивов, полученных путем преобразования текста на основе его формально-языкового теоретико-множественного описания:

 где

На основе синтагматических конструктивов могут быть построены и более сложные модели, форма которых позволяет интерпретировать их как словарно-тезаурусное описание ПОРМ.

Статистический анализ синтагматических конструктивов

Частотный и динамический анализ. Одной из задач исследования ЕЯ описания ПОРМ является получение параметрического профиля, т.е. совокупности числовых параметров генеральной совокупности. Методика проведения частотного анализа в принципе проработана и отображена в литературе [Филиппович, 1997; Филиппович, 1998].

В задачи частотного анализа входит вычисление параметров распределения слов по частоте в законе Мандельброта, а также получение количественных характеристик частотных словников. Эти параметры определяют структуру текстов, представляющих ЕЯ описания ПОРМ.

·         Построение для текстов Ti генеральной совокупности
G = (T1, T2, ..., TN) частотных функций для всех слов и парных словосочетаний. Таким образом, необходимо получить величины:

·         Построение частотных словников {S(Tj)}, где j=1,N.

·         Вычисление общего числа элементов словника: , где Rj — число элементов в словнике S(Tj).

·         Вычисление математического ожидания и дисперсии в модели “ранг–частота” для генеральной совокупности и ее элементов (текстов).

·         Нахождение параметров закона Мандельброта для генеральной совокупности.

В результате исследований должны быть получены в табличной и графической формах функции распределения и частотные словники.

Задача динамического анализа состоит в выявлении закономерностей изменения количественных характеристик структуры ЕЯ описания ПОРМ в течение времени Dt. В рамках динамического анализа рассматриваются характеристики: структуры текста; структуры, содержания и наполнения словников.

Основная идея динамического анализа заключается в наблюдении за характером изменения частотных интервалов. В общем случае имеет место следующая таблица:

Частота

F1

F2

F3

F4

....

FN

1

 

 

 

 

 

 

1 — p1

 

 

 

 

 

 

p2 – p3

 

 

 

 

 

 

...

 

 

 

 

 

 

pk — pk+1

 

 

 

 

 

 

> pk+1

 

 

 

 

 

 

Итого:

 

 

 

 

 

 

Здесь [Pk,Pk+1] — границы частотных интервалов, выбранных для наблюдения. В общем случае они могут пересекаться.

Fj — тексты или словники, по которым проводится наблюдение.

Тогда под Fj будем понимать следующее:

, если под Fj будет пониматься текст.

Необходимо отметить, что динамический анализ имеет смысл, если Tk являются ЕЯ представлением, характеризующие ПО в динамике. Так, в качестве Tk могут выступать номера журналов научного или научно-популярного еженедельника.

Динамика структуры текста показывает относительное изменение объемов частотных групп в текстах в течение некоторого интервала времени. Введем следующие обозначения:

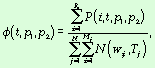 где

Здесь Mj — число слов в тексте Tj, Rt — число слов в тексте Ft.

Результаты могут быть сведены в таблицу:

Частота

F1

F2

F3

F4

....

FN

1

j (1, 0, 1)

 

 

 

 

 

1 — p1

j (1, 1, p1)

 

 

 

 

j (N, 1, p1)

p2 — p3

 

(2, p2, p3)

 

 

 

 

...

 

 

 

 

 

 

pk — pk+1

 

 

 

 

 

 

> pk+1

 

 

 

 

 

 

Итого:

 

 

 

 

1

В строке “Итого” записывается сумма вышестоящего столбца,
т.е. . Очевидно, что = 1.

Динамика структуры словников показывает относительное изменение объемов частотных групп в словниках в течение некоторого интервала времени. Введем следующие. Основное отличие от предыдущей характеристики заключается в том, что рассматриваются слова не в тексте, а в словнике, т.е. количество разных слов в частотных группах. Введем следующие обозначения:

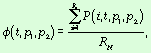 где .

Динамика содержания словников показывает соотношение объемов частотных групп в течение некоторого интервала времени. Иными словами, дает возможность выявлять закономерности распределения слов по частотным группам. Введем следующие обозначения:

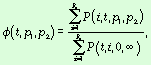 где

Здесь Rt — число слов в словнике Ft. Результаты могут быть сведены в таблицу:

Частота

F1

F2

F3

F4

....

FN

1

j (1, 0, 1)

 

 

 

 

 

1 — p1

j (1, 1, p1)

 

 

 

 

j (N, 1, p1)

p2 — p3

 

j (2, p2, p3)

 

 

 

 

...

 

 

 

 

 

 

pk — pk+1

 

 

 

 

 

 

> pk+1

 

 

 

 

 

 

Итого:

1

1

1

1

1

1

Динамика наполнения словников характеризует “прирост” новых слов в частотные группы в течение некоторого временного интервала. Характеристика позволяет оценить объемы новых слов, которые добавляются в каждый момент времени. Введем следующие обозначения:

 

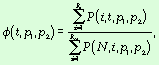
где

Здесь RN — число слов в словнике FN. Rt — число слов в словнике Ft. Результаты могут быть сведены в таблицу:

Частота

F1

F2

F3

F4

....

FN

1

j (1, 0, 1)

 

 

 

 

1

1 — p1

j (1, 1, p1)

 

 

 

 

1

p2 — p3

 

j (2, p2, p3)

 

 

 

1

...

 

 

 

 

 

1

pk — pk+1

 

 

 

 

 

1

> pk+1

 

 

 

 

 

1

Итого:

 

 

 

1

 

2.4. Парадигматическая модель текста

Словарно-тезаурусное описание ПОРМ является прежде всего результатом деятельности субъекта (субъектов). Причем эта деятельность носит упорядоченный и целенаправленный характер формализации знаний людей в форме словаря-тезауруса, она есть результат понимания реального мира. Внешняя форма словаря-тезауруса представляет собой организованный по некоторым правилам список языковых единиц различных уровней (синтагм). Получается, что словарно-тезаурусное описание ПОРМ одновременно является и синтагматической моделью некоторого текста (естественно-языкового описания ПОРМ), и образом, носителем которого являются синтагмы, а его концептные, денотативные и коннотативные компоненты в итоге знанием субъекта. Подобное представление словарно-тезаурусного описания ПОРМ позволяет поставить следующие задачи:

во-первых, представления, анализа и извлечения знаний о словарно-тезаурусном описании ПОРМ;

во-вторых, преобразования некоторого текста в его словарно-тезаурусное описание, представление естественно-языкового описания ПОРМ в форме словаря-тезауруса (назовем это преобразование “прямым”);

в-третьих, преобразования словарно тезаурусного описания в естественно-языковое описание, т.е. порождение некоторого текста (назовем это преобразование “обратным”).

Во всех трех задачах результатом их решения являются некоторые тексты, т.е. синтагматические конструкции. Рассмотрим эти задачи.

Решение первой задачи по предложенной схеме приводит к построению синтагматической модели словарно-тезаурусного описания ПОРМ. В результате этого решения получается: есть словарь-тезаурус ПОРМ (множество синтагм) — G = CTO и есть его синтагматическая модель — Stg(CTO).

Решение второй задачи приводит к появлению некоторого словарно-тезаурусного описания, которое представляет собой синтагматическую конструкцию — KSTG =Stg(G) и ее понимание или интерпретацию — I. Назовем данную конструкцию парадигматической моделью текста (естественно-языкового описания ПОРМ) и дадим ей следующее определение:

парадигматической моделью текста является представление его в виде множества основных парадигматических конструктивов, или интерпретированных синтагматических конструктивов, полученных путем преобразования текста на основе его формально-языкового теоретико-множественного описания:

 где

Такое определение делит парадигматический конструктив на две части: синтагматическую, являющуюся формально-языковым преобразованием текста, и парадигматическую, которая может быть представлена в форме естественно-языкового или формально-языкового описаний. Интерпретация парадигматического конструктива может быть представлена в словарно-тезаурусной форме, тогда получим

 где

Иначе парадигматическую модель текста можно определить как множество синтагматических моделей текста и его интерпретаций.

Анализ парадигматической модели показывает:

Во-первых, в корпус текстов могут быть добавлены какие-либо СТО, полученные до того, как начался процесс его преобразования в словарно-тезаурусное описание, а также возможно использование таких СТО на этапах интерпретации.

Во-вторых, интерпретация может касаться (быть направлена) на заранее не известную синтагматическую конструкцию, т.е. возможно перманентное преобразование исходного текста и построение тем самым множества парадигматических моделей с различными интерпретациями. Такое множество теоретически является бесконечным, но практически всегда можно назвать некоторый последний шаг преобразования, который удовлетворяет некоторому наперед заданному критерию. Если в качестве критерия рассматривать понимание так, как это предложено в [Филиппович, 2001-б], то в случае интерпретации на основе какой-либо формальной модели (в этом случае отсутствует субъектная интерпретация) всегда можно назвать некоторое целое число , которое позволит ограничить множество синтагматических преобразований и остановить процесс построения словарно-тезаурусного описания ПОРМ, или остановка может возникнуть вследствие исчерпания ресурсов, потребных для преобразований. В случае субъектной интерпретации, понимание как значение критерия носит эмпирический характер. Число, ограничивающее количество синтагматических преобразований, может быть получено при исследовании деятельности субъекта или измерением параметров и характеристик уже созданных словарно-тезаурусных описаний ПОРМ.

В-третьих, любой парадигматический конструктив, или парадигматическое преобразование текста, содержит интерпретацию субъекта, зафиксированную в некоторой форме.

Основными парадигматическими конструктивами являются словарная статья и парадигматическое отношение, на основе которых формируются словарь и тезаурус. Примерами производных парадигматических конструктивов являются: частичные словники (ограниченные неформальным признаком, например предметные), словоуказатели (предметные, именные и т.п.), конкордансы, словари, ареалы, тезаурусы и др.

На основе одного корпуса текстов могут быть построены различные производные парадигматические конструктивы, например словоуказатели, конкордансы, словари с отличающимися словарными статьями.

В качестве примеров приведем несколько вариантов [Филиппович, 1998. С.315–319]:

В предметный (терминологический) указатель могут быть включены основные термины и понятия соответствующей ПОРМ, выраженные словами, словосочетаниями (2 и 3словными). Отдельно могут быть представлены аббревиатуры. Указатель может содержать сведения об имени файла текста и номере строки от начала. При формировании предметного указателя могут использоваться другие СТО.

В именной указатель ЕЯ описания ПОРМ могут быть включены все имена собственные, встретившиеся в текстах. Указатель может содержать сведения об имени файла текста, номере страницы, номере абзаца от начала страницы и номере строки в абзаце.

Грамматический словарь ЕЯ описания ПОРМ: а) может включать слова, встретившиеся в текстовых фрагментах и относящиеся к следующим грамматическим классам: существительные, прилагательные, глаголы; б) может включать слова — наречия, числительные; в) возможно также составление полного грамматического словаря, включающего слова не только перечисленных грамматических классов, но и предлоги, междометия, союзы, частицы и местоимения. В грамматический словарь не должны включаться имена собственные, аббревиатуры, идентификаторы (слова, содержащие буквы и цифры). Грамматический словарь может иметь следующую структуру словарной статьи:

<ЛЕММА> <МИ> {s} [S],

<СЛОВОФОРМА1> <МИ1> [i1],

<СЛОВОФОРМА2> <МИ2> [i2],

...

<СЛОВОФОРМАk> <МИk> [ik].

Здесь ЛЕММА — слово в основной форме; МИ — морфологическая информация о слове (грамматический класс, подкласс); МИj — подробная грамматическая информация); s — количество словоформ в тексте; S — общее количество словоформ в тексте; ij — частота j-й словоформы.

Словарь словосочетаний ЕЯ описания ПОРМ может иметь следующую структуру словарной статьи:

<ЛЕММА>

(СЛОВОСОЧЕТАНИЕ1),

(СЛОВОСОЧЕТАНИЕ2),

...

(СЛОВОСОЧЕТАНИЕk).

Здесь ЛЕММА — слово в основной форме из грамматического словаря; СЛОВОСОЧЕТАНИЕ — двух-, трехсловное словосочетание из предметного указателя, являющееся термином или основным понятием ЕЯ описания ПО.

Конкорданс (словарь контекстов) ЕЯ описания ПОРМ может быть составлен для понятий, например, предметного указателя и иметь следующую структуру словарной статьи:

<ЛЕММА/ СЛОВОСОЧЕТАНИЕ> <КОНТЕКСТ> <АДРЕС>.

Здесь КОНТЕКСТ — ближайшее “окружение” словоформы или словосочетания, размер которого может быть выбран произвольно, однако в большинстве случаев его следует ограничить предложением (количество контекстов для одной леммы должно быть от трех до пяти, а для словосочетания достаточно одного-двух);

АДРЕС — указание на источник контекста — фрагмент текста.

Словарь определений ЕЯ описания ПОРМ может включать описание основных понятий ПОРМ, взятых из предметного указателя. Словарная статья может включать следующие сведения: заголовочное слово (понятие из предметного указателя), варианты определений (толкований) из других словарей определений, устойчивые словосочетания (из словаря словосочетаний) и 2–3 эксцерпции (примеры контекстов из текстов ЕЯ описания ПО с указанием их источника из конкорданса).

В первом и втором примерах парадигматические конструктивы “Предметный указатель” KPRD–ПУ и “Именной указатель” KPRD–ИУ получаются путем интерпретации указателя слов, являющегося синтагматическим конструктивом, образованным на основе формально-языкового преобразования текста G. Интерпретация состоит в выделении в нем “слов-предметов” и “имен”. Упрощенно, т.е. без учета операций над указателем, состоящих в расширении его за счет включения словосочетаний, упомянутого выделения аббревиатур и т.д., это имеет вид:

где StgУ(G) — указатель слов, IПУ — выбор всех слов, являющихся именами персоналий, IПУ— выбор всех слов, обозначающих предметы реального мира.

В следующих примерах парадигматические конструктивы содержат несколько синтагматических конструктивов (частотные словники и указатели) и интерпретацию (субъектную и формальную), а также включения из других СТО. Так, интерпретация в грамматическом словаре представляет собой сложную процедуру лемматизации, которая может быть выполнена различными способами, в том числе и путем формального морфологического анализа с последующим разрешением проблем омонимии непосредственно субъектом. Словарная статья словаря определений включает компоненты указателя и нескольких словарей, в том числе полученных не на основе исходного текста.

Такой подход не только оправдан, но и практически реализуем. В качестве примера можно сослаться на программное изделие Concordanses [Сидоров, 1996. С.266–300].

На основе одного корпуса текстов могут быть построены также различные тезаурусы и ареалы, в основе которых будут лежать отличающиеся друг от друга парадигматические отношения.

Парадигматическое отношение в общем виде может быть представлено как тройка формальных объектов:

 или {<синтагмаI> <отношениеR> <синтагма J>}.

Такое представление парадигматического отношения позволяет рассматривать его как элемент формального языка (сравните, например, разработки языков RX-кодов [Белоногов, 1983. С.23], так называемые X-термины и R-релатемы). Кроме этого парадигматическое отношение фактически является элементом графа — одной из формальных моделей представления знаний, на основе которой строятся многие другие (сетевые, фреймовые и т.п.).

Парадигматический конструктив, по определению, представляет собой конструкцию, состоящую из некоторого синтагматического конструктива и интерпретации, которая может быть выполнена субъектом на основе формально-языковой знаковой системы. Примерами парадигматических конструктивов отношений являются описанные ранее формальные модели оценки “силы связи” между языковыми элементами, коэффициенты . В частности, можно представить конструктив парадигматического отношения в следующем виде: , где является соответствующей интерпретацией коэффициента R.

В качестве примера рассмотрим формальное описание тезауруса в виде простой семантической сети. Элементами сети являются леммы (канонические формы слов) и коэффициенты “силы связи”, определяющие наличие связи и ее величину, измеренную в некоторой шкале.

L — простая семантическая сеть.

L = (U, V), где U — множество вершин сети (лемм), V — множество связей.

U = { u1, u2, ..., uK }, где k — число выделенных лемм.

R(ui,uj) — функция, определенная на множестве U2 — количественная мера связи между вершинами ui и uj.

Свойство

Будем считать, что запись <ui, uj> означает ориентированную связь от вершины ui к вершине uj (рис. 6):

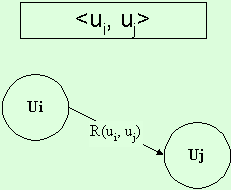
Рис. 6. Графическое представление связей между понятиями

Аналогично, как , то в общем случае .

Возникает задача построения функции R(ui,uj) на основе данных корпуса текстов. Уже было отмечено, что

Введем характеристику: |T| — число слов в тексте T, аналогично

|Сi(T)| — число слов в i-м контексте текста T.

При условии, что имеем

, где q — гранулярность разбиения, т.е. число непересекающихся контекстов, на которые разбивается текст T.

Будем считать, что |Ci(T)|=|Cj(T)|, для тогда

|T| = q|C(T)|, где С(T) — некоторый контекст из выбранных.

Поскольку С(T) тоже является текстом, то для него можно определить частотную функцию N(w,C(T)), значение которой равно числу слов w в контексте С(T). Такая частотная функция вводится на всех контекстах:

N(w,C1(T)), N(w,C2(T)),..., N(w,Cq(T)).

Будем рассматривать два слова w1 и w2, принадлежащие тексту T. Следовательно, для них можно записать два ряда:

N(w1,C1(T)), N(w1,C2(T)),..., N(w1,Cq(T)),

(3.16)

N(w2,C1(T)), N(w2,C2(T)),..., N(w2,Cq(T)).

(3.17)

Обозначим:

N(w1,C(T)) — число слов w1 в некотором контексте из числа выбранных;

N(w2,C(T)) — число слов w2 в некотором контексте из числа выбранных.

Определим функцию n(x, y), значения которой показывают число контекстов, в которых слово w1 имело частоту x, а слово w2 — частоту y.

Очевидно, что n(x,y) = n(N(w1,C(T)), N(w2,C(T))).

Представляя значения n(x,y) в табличной форме, имеем

 

N(w1,C(T))=1

N(w1,C(T))=2

...

N(w1,C(T))=R

ny

N(w2,C(T))=1

n(1,1)

n(1,2)

 

n(1,R)

 

N(w2,C(T))=2

n(2,1)

n(2,2)

 

n(2,R)

 

N(w2,C(T))=3

n(3,1)

n(3,2)

 

n(3,R)

 

...

 

 

 

 

 

N(w2,C(T))=R

n(R,1)

n(R,2)

 

n(R,R)

 

nx

 

 

 

 

 

yx

 

 

 

 

 

В таблице через R обозначена величина R = |С(T)| — размер контекста, nx — суммы по столбцам, ny — суммы по строкам, — средние значения по столбцам = .

Для построения семантической сети требуется построение корреляционной матрицы для всех имеющихся в T пар слов <wi, wj>.

В качестве меры связи между словами w1 и w2 могут, например, использоваться значения коэффициента корреляции или корреляционного отношения.

Необходимо отметить, что при построении семантической сети на основе данного ее описания нужно учесть: а) процедуру лемматизации исходного множества слов; б) размерность корреляционной матрицы RxR, точнее ее избыточность, поскольку в реальности частота слова в контексте никогда не бывает равна числу слов в этом контексте (в этом случае контекст должен был бы состоять только из одного слова), практически число R (возможную частоту слов в контексте) можно уменьшить в три раза по отношению к размеру контекста; в) гранулярность разбиения q; г) “направленность” связи.

В [Прохоров, 1999 а] описан алгоритм получения характеристик числовой связи между леммами ЕЯ описания ПОРМ, построенный на основе приведенного описания.

Парадигматический конструктив ареал представляет собой некоторую часть тезауруса, выделенную по какому-либо правилу — селективному критерию. В качестве критерия могут быть выбраны в том числе и коэффициенты “силы связи”. Самая общая постановка задачи построения парадигматических ареалов сводится к задаче кластерного анализ. В простейшем случае на рассмотренном примере представления тезауруса в виде простой семантической сети задача сводится к нахождению подграфа с заданными свойствами вершин (лемм) или дуг (коэффициентов “силы связи”).

Тезаурус, представленный в виде простой семантической сети, в общем случае является неполно связанным ориентированным графом L = (U,V) (рис. 7) с заданными множествами U = { u1, u2, ..., uN} и , V = { <ui,uj> }, а также функцией R(ui,uj) = k(ui,uj).

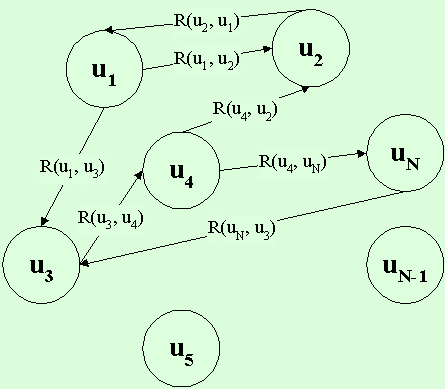
Рис. 7. Фрагмент семантической сети словаря-тезауруса

Выполним над графом L следующее преобразование: удалим из него все ребра <ui, uj>, для которых R(ui,uj)<R0 и Vij < V0: Полученный граф обозначим L(R0,V0) и будем называть приведенной семантической сетью. Смысл этой операции состоит в том, что из всей семантической сети вычленяется сеть, в которой представлены наиболее выраженные и достоверные связи. R0 и V0 являются критическими (пороговыми) значениями силы связи и числа точек в корреляционной матрице соответственно.

Поставим задачу выявления семантических ареалов в приведенной семантической сети L(R0,V0). Семантическим ареалом A в семантической сети L будем называть совокупность вершин A = {ui}, для которых выполняются следующие условия:

В итоге получаем, что в семантические ареалы входят вершины, связи между которыми “сильнее”, чем с остальными вершинами сети. Если учесть, что в качестве вершин семантической сети выступают леммы, то возможно говорить о некотором кластере, которые образуют слова в ЕЯ представлении ПОРМ.

Алгоритм построения ареалов реализован в программном комплексе ИНТЕРЛЕКС, приведен в [Прохоров, 1999], а также в гл. 3. Для лемматизации в нем используется модифицированный метод квазиоснов Ю.Н.Караулова, а в качестве коэффициентов связи — корреляционное отношение. Другой аналогичный алгоритм приведен в [Гришина, 1997].

 

7 Лингвистическая статистика, лингвостатистика, —

(1) в широком смысле — область применения статистических методов в языкознании (то есть опирающаяся на математическую статистику подсчетов и измерений при изучении языка и речи);

(2) в узком смысле — изучение некоторых математических проблем, связанных с лингвистическим материалом, главным образом с типами статистических распределений языковых единиц в тексте [ЭРЯ, 1997. Лингвистическая статистика. А.Я.Шайкевич]

8 Если строго, то N(wk, T1) + N (wk, T2) Ј N(wk, T1+T2), но тексты, как правило, завершаются стоп-знаками предложения, а значит, в этом случае возможность формирования словосочетания wk на границе T1 и T2 практически отсутствует. Ввиду малой вероятности такого события будем считать, что N(wk, T1) + N (wk, T2) = N(wk, T1+T2).