автоматизированного
Применение информационных технологий (ИТ) в прикладных областях, таких как биология, химия, педагогика, социология, психология и др., обычно проходит через два этапа. На первом этапе ИТ служат лишь инструментом, который упрощает получение результата в соответствующей области; с помощью ИТ реализуются уже известные и применявшиеся ранее методики и алгоритмы. На втором этапе ИТ играют уже не вспомогательную инструментальную роль, а служат основой для создания таких новых методик, алгоритмов, экспериментов которые без ИТ не могут быть созданы принципиально. Например, в биологии ИТ сначала стали использоваться для числовой обработки и хранения результатов экспериментов, для проведения прикладных расчетов, контроля хода экспериментов (например, круглосуточный контроль освещенности) и т.п. Все эти действия могли быть выполнены и без ЭВМ, хотя последнее, вероятно, заняло бы бóльшее время и потребовало бóльших усилий. На втором этапе, начавшемся около десяти лет назад, ИТ стали основой для таких биологических экспериментов, проведение которых каким-либо другим способом невозможно принципиально: моделирование процессов макроэволюции и видообразования, моделирование поведения внутри популяций, моделирование работы органов и механики живых организмов.
Однако, в силу специфических требований, предъявляемых в каждой области к ИТ, внедрение ИТ идет не равномерно. Если достигнутого на сегодня уровня ИТ уже достаточно для многих задач биологии, физики, химии, то в других сферах, прежде всего в гуманитарных науках – психологии, педагогике, социологии - современный уровень ИТ еще не дает возможности для широкого их применения. Например, в психологии в качестве препятствия для ИТ можно назвать отсутствие универсальных надежных методов распознавания речи, образов; в экономике – чрезмерный объем информации, которую надлежит обработать за минимальное время (проблема прогнозирования); и т.д.
В педагогике, а конкретнее в дидактике, смена этапов применения ИТ идет в настоящее время [2-5]. Это связано в первую очередь со значительным прогрессом за последние годы ИТ в области сетевых технологий (глобальное распространение сети Интернет) и в области хранения и переработки данных (для многих задач это сняло ограничения по доступности дисковых и процессных ресурсов).
Т.о. представляет необходимым и актуальным провести анализ ИТ применительно к процессу обучения; выделить особый класс автоматизированных систем обучения, которые не сводятся только к поддержке процесса обучения, а вносят в него принципиально новые, недоступные в другой случае, аспекты [1].
В данной статье в самом общем виде представлена попытка указать направление такого анализа применимости ИТ в процессах обучения; дается обзор тех ключевых новшеств, которые возникают по привлечению ИТ к процессу обучения; рассматривается ряд конкретных вариантов применения ИТ.
Применение ИТ в ходе процесса обучения можно наиболее обще разделить на совместное (или групповое) и индивидуальное. В индивидуальном случае ИТ служат непосредственно только для одного, данного субъекта (человека) – например, автоматизация проверки выполненных заданий. При смешанном (групповом) применении, ИТ служат связующим звеном между различными субъектами – например, при организации и проведении телеконференций между физически удаленными друг от друга людьми. В свою очередь индивидуальный вариант также распадается на несколько, в зависимости от цели его использования: переработка (формы представления) информации - например, проверка выполненных ранее заданий; извлечение информации из субъекта – например, автоматическое тестирование; выдача информации субъекту - автоматическое консультирование. Совместное (групповое) применение, в зависимости от охвата и взаимной удаленности субъектов, условно делится на локальное и глобальное.
Уже в рамках такой простейшей классификации можно выделить ряд автоматизированных систем обучения (АСО) и указать их взаимосвязь друг с другом. Например, видно, что система “мультимедийный учебный курс” является по большей части индивидуальной и ориентированной на выдачу информации субъекту; а системы дистанционного обучения во многом смешанные – сочетают в себе как индивидуальное, так и групповое применение и обладают обратной связью.
Также и ключевые новшества, вносимые ИТ, можно рассматривать в рамках предложенной классификации, опираясь на уже достигнутое при инструментальном использовании ИТ (т.е. на достигнутое на первом этапе). По сути, следует указать, во что перерастет “потолок” первого, инструментального этапа, и классифицировать полученное из него “основание” второго этапа. В виду обширности такого анализа, укажем и рассмотрим более подробно только некоторые направления. В частности:
· извлечение знаний в ходе автоматизированного тестирования;
· автоматизированная проверка результатов обучения;
· проведение лабораторного практикума.
Кратко можно перечислить и другие варианты применения ИТ в процессе обучения: усиление обратной связи Обучающий-Обучаемый (пример: в ходе занятия в оперативном режиме Обучающиеся высказывают свое мнение о читаемом материале, например о его сложности, не прерывая самого изложения материала. В дальнейшем полученные замечания анализируются для внесения определенных уточнений в излагаемый материал); индивидуализация представляемой информации для каждого Обучающегося; оперативная обработка результатов (мониторинг множества параметров-факторов учебного процесса и их статистическая обработка и прогнозирование); автоматизация генерации информации (например, автоматический подбор современной актуальной информации (без участия Преподавателя), для использования ее в качестве задач или примеров в ходе учебного процесса); автоматизация составления и детализация учебных планов (вплоть до создания индивидуальных учебных планов, содержащих индивидуальные задания); и др.
Отдельные вопросы применения ИТ
Среди всего множества аспектов применения ИТ в образовании более подробно в данной статье рассматриваются, как уже было сказано, только три. Их выбор обусловлен желанием продемонстрировать разносторонность и широту применения ИТ. Фактически, три представленных вопроса охватывают собой элементарный трехэтапный учебный процесс: лабораторная работа – тестирование-проверка результатов ее усвоения – оценка результатов. Наибольшее внимание уделено вопросу использования ИТ при извлечении знаний в ходе автоматизированного тестирования.
Во многих случаях проведение лабораторного практикума обычными средствами невозможно. Например: практические занятия в медицине; сложные и дорогостоящие эксперименты в физике, химии; длительные наблюдения в астрономии. Однако полный отказ от таких занятий также невозможен – во многих науках наибольшую ценность имеет именно практический опыт, который должен быть получен при обучении.
На первом этапе решением послужили испытательные стенды-макеты, имитирующие реальные процессы. Чтобы показать, что принципиально нового внесено ИТ, пришедшим на смену традиционным стендам-макетам, достаточно перечислить устраненные ими недостатки таких макетов:
· жесткий алгоритм работы – в большинстве случаем для смены алгоритма работы требовалось заменить весь макет целиком;
· высокая специализация макета – нацеленность его только на отдельную функцию (эксперимент, реакцию) и игнорирование смежных функций;
· статичность – невозможность использовать опыт работы с данным или аналогичным макетом других лиц;
· низкая реалистичность – ограниченность применимости полученных и отработанных навыков, результатов на практике;
· ограниченное количество результирующей и сопроводительной информации.
Как характерный пример внедрения ИТ, можно привести учебные военные тренажеры. Современные военные тренажеры (танков, вертолетов, других боевых машин) в сравнении со своими предшественниками отличаются высокой реалистичностью, возможностью всестороннего контроля и анализа, как хода виртуального боя, так и его отдельных частей, результата в целом. Такие тренажеры обычно связанны в группы, обмениваются информацией между собой и с центральной БД – что дает возможность отрабатывать совместные действия многим участникам виртуального боя. Уже на современном этапе такие системы дают результаты, сравнимые с результатами реальных учений, а в перспективе позволят осуществлять дистанционное ведение боевых действий.
Другой проблемой в ходе обучения является необходимость оценки и контроля его результатов. Особенно важным это становится в случае дистанционного обучения, где непосредственная личная работа Преподавателя с Обучаемым сведена к минимуму. Причем, для точной оценки результатов важно не только непосредственное оценивание, но и само их получение - извлечение сведений из Обучающегося - этот второй аспект рассмотрен в следующем разделе, а в данном разделе основное внимание уделено непосредственной оценке результатов.
В большинстве случае результаты обучения выявляются как результаты решения одного или нескольких заданий. Результаты можно отнести к одной из трех групп:
· тестовые результаты – результаты ответов на вопросы теста, где обучающийся выбирает один или несколько правильных ответов из группы предложенных ответов. Автоматизированная их проверка тривиальна – достаточно сравнить два множества: множество номеров ответов обучающегося и множество номеров правильных ответов.
· текстовые результаты – результаты самостоятельного составление ответа Обучающимся, причем ответа в письменной (текстовой) форме.
· прочие результаты – результаты самостоятельного составления ответа Обучающимся, кроме письменной формы (устный ответ, схема, чертеж и т.п.). Общих методы автоматизации их проверки в настоящее время не существует, что обусловлено ограничениями существующих методов распознавания, т.е. фактически перевода сведений извлеченных из обучающегося в электронную форму с учетом последующей необходимости в выделении смысла.
Проверка письменных (текстовых) и прочих результатов в общем случае требует выделения смысла. Т.е. проверка идет не путем сравнения полученных результатов с образцом (как в случае тестовых результатов), а требуется сначала представить результат в некотором формализованном виде. Например: в случае письменных результатов, очевидно, что невозможно хранить все мыслимые варианты ответа на вопрос “Как перемножить два натуральных числа X и Y” и что необходимо хранить один вариант ответа, а все остальные варианты пытаться свести к нему. Если правильный ответ “X*Y”, а ответ обучающегося, например, есть: “нужно сложить X сам с собой (Y-2)-раз”, то необходим алгоритм, который позволит свести такой ответ к формальной форме (алгоритм формализации); и если результат работы алгоритма будет не равен “X*Y”, а в данном случае мы получим “X*(Y-2)”, то такой ответ неправилен. В случае устных и графических результатов дополнительной трудностью является еще и необходимость их хранения в виде, доступном для последующей обработки, для последующего применения алгоритма формализации.
Все это сдерживает внедрение ИТ, а предпринимавшиеся попытки использования ИТ для анализа результатов не тестовой природы надо признать неудачными. Особенно это проявилось (например) в случае программ обучения иностранным языкам – в них для проверки произношения пришлось вернуться к традиционным методам (Обучающийся слушает свою речь и речь-образец и сравнивает их на слух самостоятельно).
автоматизированного тестирования
Этапом, предшествующим проверке результатов, очевидно, является этап их получения. Здесь применение ИТ пока носит инструментальный характер. Однако, по мнению автора данной работы, в настоящее время реализуемо (хотя возможно только на проектном алгоритмическом уровне) и автоматизированное извлечение знаний. Представленный ниже алгоритм служит иллюстрацией возможности такой реализации.
Неформально решаемую задачу по извлечению знаний можно сформулировать следующим образом: требуется выдавать Тестируемому вопросы, начиная с самых сложных, причем сложность выдаваемых вопросов нужно изменять в зависимости от правильности ответа на предыдущие (заданные ранее) вопросы; число вопросов заранее не известно и лимитируется некоторым уровнем, достижению которого служат ответы тестируемого.
Оценивание Тестируемого возможно следующим способом: задавать вопросы до тех пор, пока в сумме они не дадут некоторый пороговый уровень (например: пока не будут рассмотрены все разделы того предмета, по которому идет тестирование) и на основании числа правильных-неправильных вопросов (а также, учитывая их число в каждом разделе) выставить оценку.
Задачу можно упростить, наложив ограничения, применяемые всюду на практике; а именно, будем полагать что:
· Тема, по которой проводится тестирование, состоит из N1 разделов верхнего уровня;
· Разделы организованны древовидно и не пересекаются; максимальная глубина разделов известна:
![]() (3.1)
(3.1)
· Вопросы относящиеся к разделу верхнего уровня Q(1)j не относятся ни к какому другому разделу верхнего уровня Q(1)k (вопрос относится к разделу – если он рассматривается в данном разделе или в любом из его подразделов)
· В пределах одного раздела верхнего уровня вопросы могут относиться одновременно к разным его подразделам
· Существует некоторый минимальный по сложности вопрос, все другие вопросы кратны ему по сложности
Примером первого и второго ограничения может служить организация любой книги – в ней каждая страница относится только к одному разделу некоторого уровня (т.е. одна и та же страница не может относится одновременно, например, к двум главам).
Схематично это показано на рис.1, где под Q(i)j понимается j-ый раздел (i)-ого уровня. Например: Q(1)1 – глава 1, Q(1)2 - глава 2; Q(2)1 - параграф 1, Q(2)2 - параграф 2 и т.д.
|
Q(1)1 |
Q(1)2 |
. . . . . |
Q(1)N1 |
||||||||
|
Q(2)1 |
Q(2)2 |
Q(2)3 |
Q(2)4 |
Q(2)N2 |
Q(2)N2+1 |
Q(2)N2+2 |
|||||
|
|
|
Q(3)1 |
Q(3)2 |
Q(3)3 |
|
|
|
|
|||
|
|
|
Q(4)1 |
Q(4)2 |
|
|
. . |
. . |
. . |
|||
|
|
|
|
Q(5)1 |
Q(5)2 |
|
|
|
|
|
||
Рис. 1. Пример организация разделов Q(i)j
Тогда (3.1), например, будет:
Q(1)2 = Q(2)3 U Q(2)4;
Q(2)3 = Q(3)1U Q(3)2 U Q(3)3
Q(3)1 = Q(4)1U Q(4)2
Q(4)2 = Q(5)1U Q(5)2
Формализуем (в первом приближении) задачу, основываясь на данном выше описании.
1. Под величинами Q(i)j понимаются веса разделов. Веса должны отражать относительную сложность разделов (например: они могут быть пропорциональны времени изучения раздела). Будем считать веса целыми числами. Для любого раздела: Q(i)j > Q(i+1)k (вес раздела больше веса любого из его подразделов).
2. До начала тестирования задается общая сложность теста Q (в тех же единицах что и сложности разделов).
3. Т.к. вопросы внутри разделов верхнего уровня независимы, то первым шагом отбираются разделы для тестирования среди всех доступных разделов. В сумме они по весу должны или точно равняться Q, или незначительно (q) превосходить Q:
 (3.2)
(3.2)
где xij=1, если раздел был выбран для теста, иначе xij=0
Если выбран раздел верхнего уровня, то его подразделы не выбираются (т.к. они считаются фактически уже выбранными). Выбор следует производить сверху вниз (т.к. тогда выше вероятность, что вопросы выбранного раздела не потребуют для ответа на них знаний из не выбранных разделов).
Пример: на (рис.2) выбранные разделы показаны цветом.
4. Выбор вопросов упорядочен – сначала задаются относительно трудные вопросы, если на них не последовало ответа – задаются более легкие вопросы, если нет ответа и на них – еще более легкие и т.д. По возможности, вопросы не должны содержать повторов (т.е. при выборе очередного вопроса он должен min пересекаться [или, что то же самое, max отличаться] с уже заданными вопросами). Но при этом большая часть вопроса должна относиться к выбранному разделу: задание вопроса целиком лежащего в невыбранном разделе не допускается.
|
Q(1)1 |
Q(1)2 |
. . . . . |
Q(1)N1 |
||||||||
|
Q(2)1 |
Q(2)2 |
Q(2)3 |
Q(2)4 |
Q(2)N2 |
Q(2)N2+1 |
Q(2)N2+2 |
|||||
|
|
|
Q(3)1 |
Q(3)2 |
Q(3)3 |
|
|
|
|
|||
|
|
|
Q(4)1 |
Q(4)2 |
|
|
. . |
. . |
. . |
|||
|
|
|
|
Q(5)1 |
Q(5)2 |
|
|
|
|
|
||
|
|
|
|
← Q → |
|
|
|
|
|
|
Рис. 2. Пример выбора разделов Q(i)j
Алгоритм рюкзака
Среди существующих алгоритмов, одним из наиболее близких к искомому нами (см. далее), является алгоритм решающий “проблему рюкзака” (bin packing problem, the subset-sum problem) [9, гл.19; 6, 34.5.5; 7, ch.5]:
Требуется найти (если это возможно) коэффициенты xi,
равные 0 или 1, такие, что для заданного числа S и заданного множества
A={a1, a2, …, an} выполняется равенство:
![]()
т.е., формулируя словесно: требуется решить какие из n предметов, весом ai единиц каждый, мы должны взять, чтобы в точности заполнить рюкзак грузоподъемностью S единиц.
В общем случае “проблема рюкзака” является NP-полной [8,9,6,11,12] - т.е. для нее не найден алгоритм, оптимально решающий ее за полиномиальное время, но не доказано и то, что такого алгоритма вообще нет (“проблема P=?=NP”). В частном же случае, были предложено множество алгоритмов, решающих “проблему рюкзака” при некоторых ограничениях или при специальном виде исходных данных. Особенно задача упрощается для случая “сверхвозрастающего рюкзака” [9]:
исходное множество A удовлетворяет дополнительному условию
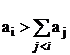 для
всех i от 1 до n
для
всех i от 1 до n
т.е., формулируя словесно: если предметы упорядочены по их весу ai от самого легкого до самого тяжелого, то тогда каждый предмет i должен быть тяжелее, чем суммарный вес всех предыдущих предметов.
тогда “сверхвозрастающий рюкзак” заполняется за линейное время по следующему алгоритму:
Шаг 1. i = n
Шаг 2. если ( i >= 1 ) то
если ( S > = ai ) то
S = S-ai
xi = 1
иначе
xi = 0
все_если
иначе
выход_из_алгоритма:
если S не 0, то решения нет;
иначе {xi} - решения
все_если
Шаг 3. i = i –1
Шаг 4. перейти к шагу 2
(словами: пытаемся положить в рюкзак самый тяжелый предмет, если это не удалось – рюкзак с уже имеющимся его содержимым не выдержит по весу предлагаемый предмет - то переходим к следующему предмету с меньшим весом).
“Не сверхвозрастающие, или нормальные, рюкзаки представляют собой трудную проблему - быстрого алгоритма для них не найдено. Единственным известным способом определить, какие предметы кладутся в рюкзак, является методическая проверка возможных решений, пока не найдется правильное. Самый быстрый алгоритм (принимая во внимание различную эвристику) имеет экспоненциальную зависимость от числа возможных предметов” [9].
Алгоритм выбора раздела можно свести к алгоритму рюкзака, причем попытаться (в каждом конкретном случае) сделать алгоритм линейным: это достигается благодаря наличию величины q: в выражении (3.1), а также благодаря тому, что выборка идет сверху вниз и что без предварительной выборки верхнего уровня нижние уровни недоступны. Можно заменить объединение на сумму весов; все выбранные веса в сумме удовлетворят условию (3.2) – т.о. к ним будет применим алгоритм рюкзака. Однако, т.к. по условию разделы верхнего уровня независимы, то алгоритм рюкзака надо применять к каждому уровню отдельно, раскрывая уровень на подуровни если не удалось набрать требуемую сумму Q ограничиваясь только данным, рассматриваемым уровнем. Выборку самих разделов верхнего уровня следует вести эмпирически, например, начиная с самого тяжелого (с самым большим весом) или случайным образом.
Например:
1) отсортировать веса по уровням и в пределах верхнего уровня;
2) выбрать веса среди весов верхнего уровня, т.е. из множества Q(1)j для заполнения до (Q - сумма_уже_выбранных_весов); если среди них имеются одинаковые, то берем любой;
3) повторять 2 пока это возможно;
4) выбрать веса среди разрешенных, следующих за верхним уровнем, - т.е. из множества Q(2)j для заполнения до (Q - сумма_уже_выбранных_весов); если среди них имеются одинаковые (в пределах одного вышележащего раздела), то берем любой;
5) повторять 4 пока это возможно.
…
Пример:
Веса разделов представлены на рис.3; Q = 9, q=1/9, Qq=Q(1+q)=10
|
|
2 |
9 |
3 |
||||||||
|
|
1 |
1 |
8 |
1 |
1 |
1 |
1 |
||||
|
|
|
|
4 |
1 |
3 |
|
|
||||
|
|
|
|
2 |
2 |
|
|
|
||||
|
|
|
|
|
1 |
1 |
|
|
|
|||
Рис. 3. Пример выбора разделов Q(i)j
Тогда:
1. Среди верхнего уровня {2,9,3} берем, например, 2 (случайная выборка); т.к. 2 < 10 то нужен следующий шаг
2. Среди оставшихся {9,3} берем 9; не подходит т.к. (2+9)=11 > 10
3. Среди оставшихся берем 3 т.к. (2+3)=5 < 10 подходит, а других весов на верхнем уровне нет
|
2 |
9 |
3 |
||||||||
|
1 |
1 |
8 |
1 |
1 |
1 |
1 |
||||
|
|
|
4 |
2 |
2 |
|
|
||||
|
|
|
2 |
2 |
|
|
|
||||
|
|
|
|
1 |
1 |
|
|
|
|||
4. Т.к. разделы “2” и “3” уже выбраны, то дальше выборка идет только среди разрешенных разделов, т.е. внутри “9” (т.к. можно считать, что вместе с “2” и “3” выбраны и все их подразделы лежащие ниже)
5. Среди составляющих “9” подразделов {8,1} подходит только “1” (т.к. (5+8)=13 > 10 и тем более (6+8)=14 > 10) [если бы выбрали “1” раньше “8”]
6. Т.к. раздел второго уровня “1” выбран, а единственным разрешенным остался раздел “8”, то смотрим в нем
|
2 |
9 |
3 |
||||||||
|
1 |
1 |
8 |
1 |
1 |
1 |
1 |
||||
|
|
|
4 |
1 |
3 |
|
|
||||
|
|
|
2 |
2 |
|
|
|
||||
|
|
|
|
1 |
1 |
|
|
|
|||
7. Имеем к данному шагу: (2+3+1)=6 < Qq и среди {4,1,3} составляющих “8” выбираем, например, 1: (6+1)=7 < 10
8. Дальше, из {4,3} выбираем, например, 4 - не подходит: (7+4)=11>10
9. Осталось (для второго уровня) только 3: (7+3)=10 = Qq - подходит, процесс завершается:
|
2 |
9 |
3 |
||||||||
|
1 |
1 |
8 |
1 |
1 |
1 |
1 |
||||
|
|
|
4 |
1 |
3 |
|
|
||||
|
|
|
2 |
2 |
|
|
|
||||
|
|
|
|
1 |
1 |
|
|
|
|||
На практике, при большом числе разделов и их дроблении, процесс обычно всегда сходится. Сходимости способствует и требование на нестрогое соответствие набранного веса величине Q – достаточно попадания в диапазон [Q;Qq].Особенно в случае если (Q-Qq) ≥ 1, а вес наименьших разделов равен 1 (тогда высока вероятность того, что выборка “1”-разделов позволит попасть в диапазон [Q;Qq] ).
После выбора разделов, необходимо выбрать вопросы внутри каждого из разделов. Существенным здесь является то, что вопросы выбираются по ходу тестирования и процесс из выборки и составляет важную и неотъемлемую часть самого тестирования (тогда как выбор разделов происходит до начала тестирования).
Формализуем задачу:
Определим:
· Вопрос k непосредственно относится к разделу Q(i)j если большая часть вопроса лежит в пределах раздела Q(i)j, и не лежит в пределах никакого другого подраздела раздела Q(i)j.
· Вопрос k на прямую относится к разделу Q(i)j если большая часть вопроса лежит в пределах раздела Q(i)j.
· Вопрос k относится к разделу Q(i)j если какая-то часть вопроса лежит в пределах раздела Q(i)j.
Например:
|
|
2 |
9 |
3 |
||||||||||||||
|
|
1 |
1 |
8 |
1 |
1 |
1 |
1 |
||||||||||
|
|
|
|
|
|
4 |
|
|
|
1 |
3 |
|
|
|
||||
|
|
|
|
2 |
2 |
|
|
|
||||||||||
|
|
|
|
|
1 |
1 |
|
|
|
|||||||||
Рис. 4. Пример принадлежности для вопроса k
На рис.4 вопрос k непосредственно относится к разделу с весом 4, напрямую относится к разделам с весом 4, 8, 9 и просто относится к разделам с весами 4,8,9,2,2. Очевидно, что чем сложнее вопрос, тем к более высокому уровню он относится непосредственно. (Принадлежность вопросов к тем или иным разделам задается при создании самого вопроса.)
Выборка вопросов ведется по следующим принципам:
· выбираются вопросы непосредственно относящиеся к выбранным разделам (сверху вниз), начиная с самого сложного
· выбранные вопросы должны полностью покрыть выбранные разделы (хотя, возможно, они покроют [частично] и другие разделы)
· все вопросы, относящиеся к некоторому разделу верхнего уровня, образуют покрытие (из которого, по ходу тестирования, и выбираются вопросы). Выборка каждого вопроса автоматически удаляет из покрытия и другие вопросы, составляющие часть выбранного.
Из данного описания видна схожесть алгоритма выбора вопросов с алгоритмом выбора разделов или с алгоритмом рюкзака. Такая связь становится более заметной, если рассматривать случай, когда выбрано несколько идущих подряд разделов. Например, если выделить последовательные части (относящиеся к каждому из разделов верхнего уровня) из примера предыдущего раздела, то получим:
|
|
2 |
|
3 |
||||||||||||
|
|
|
|
|
1 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
1 |
3 |
|
|
|
||
или, рассматривая, например, независимый раздел верхнего уровня с весом “9” (и все его выбранные составляющие):
|
|
|
1 |
3 |
1 |
|
Пусть сюда (в рамках раздела “9”) относятся вопросы K={ k1=3, k2=2, k3=5, k4=7, k5=3 } (вопросы показаны для наглядности один над другим без пересечения друг с другом; все отмеченные области во второй строке относятся к k4; аналогично в третьей строке – к k5).
|
|
k1 |
|
k2 |
k3 |
||||||
|
|
|
|
k4 |
|
|
|
|
|
|
|
|
|
|
|
k5 |
|
|
|
|
|
|
|
Выборка вопросов начинается с самого сложного. Будем писать +ki если на вопрос ki последовал правильный ответ и -ki иначе. Для осуществления выборки вопросы предварительно организуются в дерево (по их вкладу в покрытие, т.е. по их сложности; но с учетом других элементов – например, см. ниже, при правильном ответе +k4 нет необходимости задавать вопрос k3, т.к. перекрытие +k3 и +k4 значительно, а единственной причиной для вопроса k3 может служить желание организовать полное покрытие всех выбранных разделов “1”, “3”, “1”). Ответы +/-ki фактически соответствуют навигации (перемещению) по выстроенному дереву. Т.о. основной задачей является задача построения дерева вопросов. Например, в рассматриваемом случае (цифры под листьями дерева означают: “вес_не_покрытой_области; вес_перекрывающейся_облас-ти”) получаем (рис.5).

Рис. 5. Пример дерева вопросов
На основе рассмотренных вопросов, можно заключить, что внедрение ИТ в процесс обучения будет усиливаться с каждым годом. Этому будет способствовать как рост запросов к качеству и срокам обучения, так и рост возможностей самих ИТ [2,5]. Поэтому представляется крайне важным не упустить данный процесс, вовремя создать научные и практические разработки в этой области - что позволит выйти в лидеры в сфере образования, а значит и подготавливать кадры самой высокой квалификации.
1. [ГосНИИ ИТТ "Информика", 2003].
10. [Шень А., 1995]
11. [Ахо А., 1979]
12. [Гэри М., 1962]