А.Л. Волков
Тайна за семью печатями
“Свет мой, зеркальце!
скажи
Да всю правду доложи:
Я ль на свете всех милее,
Всех румяней и белее?”
А. С. Пушкин
Интересно, что ответит случайный прохожий на улице, если у него спросить: А что же такое искусственный интеллект? Если в первый момент он не подумает, что Вы сумасшедший, то по лицу его разольется недоумение, перерастающее в растерянность. Решившись же ответить, этот несчастный, застигнутый Вами врасплох, с вероятностью 0.99 скажет: “А… это когда компьютер думает…”.
Интуитивно это, конечно же, так, но подобное понимание вопроса создает довольно забавную ситуацию. Существует Большинство, имеющее именно такое представление об искусственном интеллекте, и Меньшинство, знающее, что конкретно скрывается или, вернее, не скрывается за этим понятием. Да что уж тут говорить, если общепринятого понятия до сих пор как такового нет. Большинство считает, что искусственный интеллект – это тайна за семью печатями, не доступная простому смертному, удел избранной касты – Меньшинства, которые являют собой элиту – голубая кровь, белая кость, если хотите – компьютерного сообщества. Меньшинство же, по вполне понятным причинам, далеко не всегда стремиться разубедить в этом доверчивое Большинство.
Давайте же, вооружившись элементарной логикой, попробуем сорвать все семь печатей, скрывающих технологии искусственного интеллекта от наших не всегда скромных, жадных до знаний взглядов.
Прежде всего, давайте определимся с самим термином. Итак, под искусственным интеллектом будем понимать совокупность программных и аппаратных средств, использование которых должно приводить к тем же результатам, к которым при решении данного класса задач приводит интеллектуальная деятельность человека. Здесь сразу же следует еще раз подчеркнуть, что систему искусственного интеллекта можно рассматривать только в контексте решения данного класса задач, а чаще – всего лишь одной задачи. Это означает, что все остальные задачи система может вообще не уметь решать.
Существенная оговорка, не правда ли? Ведь, по сути, это означает, что мы пытаемся разработать модель, имитирующую работу человеческого мозга, только для решения некоторой заранее четко сформулированной задачи, не претендуя на создание комплекса программно-аппаратных средств, воспроизводящего работу мозга в целом.
Но даже при таком ограничении задача остается титанической. Можно предложить два пути ее решения. Первый – посмотреть на то, как работает человеческий мозг и сделать также, или, хотя бы, похоже. Решение было бы именно таким, если бы на Земле кто-нибудь дерзнул бы утверждать, что абсолютно все знает о работе мозга. Такого специалиста, к сожалению, пока нет. Но, несмотря на это, идея оказалась настолько привлекательной, что на ее основе была создана нейробионическая теория искусственного интеллекта. Данная теория рассматривает вопросы разработки и использования в рамках систем искусственного интеллекта нейронных сетей – структур, реализующих наше представление о работе мозга. Это направление на сегодняшний день является наиболее перспективным, но у него есть существенный недостаток – высокая ресурсоемкость и довольно сложность реализации конечных изделий. Этот недостаток делает невыгодным использование нейронных систем для решения относительно простых задач.
Второе направление в теории создания систем искусственного интеллекта, которое, кстати, доминировало до разработки теории нейронных сетей – это теория экспертных систем. Если в нейробионическом направлении разработчики пытаются формализовать работу мозга и посредством этого решить задачу, то в направлении, связанном с экспертными системами, формализуется непосредственно решение задачи. Это позволяет не затрагивать сложные материи организации работы мозга, а сконцентрироваться на построении математической модели самой задачи.
Вы, вероятно, уже заметили, что большинство вопросов, которые пока были поставлены, довольно далеки от техники, но зато носят ярко выраженных философский характер. Действительно, занимаясь проблемами искусственного интеллекта нельзя ограничиваться только сугубо техническим подходом. В связи с этим позволю себе следующую аналогию. Когда в древнем мире зарождалась физика, она настолько переплеталась с философией, что порой между ними трудно было найти вообще хоть какую-нибудь границу. По сути физика была частью философии, касавшейся реального мира. Тогда люди пытались понять, как устроен окружающий их мир. Сейчас ситуация почти аналогична, только мы находимся на другом витке познания. Возомнив себя всемогущим, решив, что окружающий мир уже познан, человек с удивлением обнаружил, что для него единственной и неразрешимой пока загадкой остался он сам! Люди столкнулись не только с новыми богатыми возможностями, которые может предоставить им использование искусственного интеллекта, но и с новым мировоззрением, новыми этическими и социальными проблемами. Именно поэтому, человечеству еще предстоит выработать философский подход к данному вопросу.
Итак, осталось немногое – нужно проанализировать работу своего мыслительного аппарата при решении поставленной задачи и запрограммировать полученный алгоритм. Тут находится еще один подводный камень. Думая, Вы не всегда можете точно сказать, каким именно образом Вы приходите к тому или иному результату. Простейшим примером тому может служить то, что Вы сейчас делаете. Я не волшебник, но попытаюсь угадать – ага, Вы читаете мою статью! Скажите, а как Вы понимаете то, что здесь написано? Для кого-нибудь члена далекого племени Умба-Юмба эти строки представлялись бы как набор загадочных рисунков, а для Вас они наполнены смыслом. Теперь приведу несколько более изощренный пример. Прочитайте слово “ЗАМОК”. А теперь скажите, на каком слоге Вы поставили ударение, и почему Вы его поставили именно там. Можно привести еще массу таких же забавных примеров, способных рассмешить своей кажущейся простотой, сочетающейся с невозможностью или крайней сложностью их формализации.
Таким образом, приходим к выводу, что помимо четкой логики, о которой забывать никак нельзя, в нашем мышлении присутствует некоторая трансцендентная составляющая - интуиция, предчувствие, опыт или что-то в таком духе. С одной стороны это значительно осложняет задачу, потому что становится не достаточно одной формальной логики, а с другой упрощает ее. Это упрощение состоит в следующем: давайте не будем рассматривать абсолютную истину, которой по нашим предположениям нет. Вместо нее в качестве истины примем мнение эксперта в рассматриваемой области. Качество экспертной оценки системы, построенной на основе вышесказанного, будет определяться компетентностью эксперта.
При такой постановке, задача сводится к формализации знаний эксперта. Под знаниями следует понимать не только данные, то есть голые факты, но и алгоритмы их обработки. Решению именно этой задачи и посвящена теория создания экспертных систем, то есть систем, построенных на знаниях экспертов.
В качестве определения экспертной системы, на мой взгляд, лучше всего взять определение, данное Крисом Нейлором. Оно звучит следующим образом: под экспертной системой понимается система, объединяющая возможности компьютера со знаниями и опытом эксперта в такой форме, что система может предложить разумный совет или разумное решение поставленной задачи.
При таком подходе центральной проблемой становится разработка формальной модели представления знаний. Модель представления знаний, рассматриваемая как ядро экспертной системы, должна определять тип используемых данных, методы их структурирования и способы задания логических связей между ними. В зависимости от этого различают следующие виды формальных моделей представления знаний:
 |
|
Рис. 1.
Классификация моделей представления знаний
|
Мы подробно остановимся на трех из вышеперечисленных моделей: модель логики высказываний, продукционная модель и фреймовая модель. Выбор именно этих моделей не случаен. Некоторое время назад мною была разработана система, реализующая именно эти модели, как наиболее простые для понимания и, в то же время, позволяющие реализовать в своих рамках большинство типичных задач экспертных систем.
В этой статье, уже достаточно утомив Вас своими мыслями, я хотел бы поделиться своим личным опытом в разработки экспертных систем и немного рассказать о достигнутых мной самим результатах.
Разработанная мной система называется “Эксперт”. Она представляет собой инструмент для разработки экспертных систем двух видов: основанных на модели Нейлора (продукционная модель) и основанных на логике высказываний. Модель фреймов используется “Экспертом” как вспомогательная и служит для осуществления диалога с пользователем.
Модель Нейлора реализует представление знаний в виде неточных продукционных правил. Продукционное правило представляет собой выражение вида [2]:
УСЛОВИЕ ® ДЕЙСТВИЕ,
в котором левая часть (антецедент) описывает определенную ситуацию, а правая (консеквент) – действие, выполнение которого предполагается в случае обнаружения ситуации.
Пусть имеется Н = {Нi} – множество целей (гипотез), которые необходимо оценить и С = {Сj} – множество понятий или условий (свидетельств), на базе которых производится эта оценка. Тогда в качестве знаний используется множество правил вида [2]:
Cj ® Cj+1 и Cj+1 ® Hi.
Одного из существенных достоинств продукционных систем является возможность использования вероятностных характеристик, задающих коэффициент уверенности или меру доверия. При этом значение любой логической переменной: гипотезы или свидетельства, в общем случае есть вероятностная величина и лежит в диапазоне [0, 1]. Использование неточных знаний предполагает наличие специальных математических методов. В основе одного из таких методов лежит теорема Байеса.
Пусть Н – событие, заключающееся в том, что данная гипотеза верна. Пусть Е – событие, заключающееся в том, что наступило определенное доказательство (свидетельство), которое может или не может подтвердить правильность указанной гипотезы.
Тогда:
Р(Н) – вероятность того, что событие Н истинно;
Р(Е) – вероятность того, что событие Е произошло.
Если вероятность равна нулю, то данное событие не произойдет никогда. Если же вероятность равна единице, то данное событие происходит всегда.
Р(не Н) = 1–Р(Н) – вероятность того, что событие Н ложно.
Два события независимы, если вероятность их совместного наступления равна произведению вероятностей наступления каждого из событий в отдельности.
Р(Е1&Е2) – совместная вероятность наступления как события Е1, так и события Е2.
Р(Н: Е) – условная вероятность наступления события Н, определяемая с учетом того, сто событие Е уже наступило. Если события Н и Е независимы, то Р(Н: Е) = Р(Н).
В общем случае [1]:
|
|
(1)
|
Аналогично [1]:
|
|
(2)
|
поэтому [1]:
|
|
(3)
|
С учетом введенных обозначений теорема Байеса имеет следующий вид [1]:
|
|
(4)
|
В начале может показаться, что всегда имеет смысл применять вероятность Р(Н: Е), ведь мы хотим знать, какова вероятность того, что гипотеза Н верна при наступлении данного свидетельства, а не наоборот. Задача заключается в том, что Р(Н: Е) порой вовсе не очевидна. Если известна Р(Н: Е), то нет необходимости в экспертной системе, целью которой будет вычисление этого самого Р(Н: Е). Вероятность же Р(Е: Н), напротив, является величиной более очевидной, если учитываются данные по рассматриваемой проблеме.
Для двух или более событий Е1 и Е2 справедливо следующее: если Е1 и Е2 независимы, то Р(Е1 & Е2: Н) = Р(Е1: Н) Р(Е2: Н).
Ошибочным является утверждение о том, что
Р(Н: Е1 & Е2) = Р(Н: Е1) Р(Н: Е2).
Если Е является событием, заключающимся в том, что “все Еi наступили” и, кроме того, они все не зависят друг от друга, то можно вычислить [1]:
|
|
(5)
|
|
|
(6)
|
Предположим, что существует некая гипотеза Н и некоторое подтверждающее или не подтверждающее ее свидетельство, которое обозначим через Е, тогда:
Р(Н) – априорная вероятность истинности гипотезы Н. Это вероятность наступления Н без учета факта существования Е;
Р(Н: Е) или Р(Н: не Е) – апостериорная вероятность гипотезы Н, т.е. вероятность Н при условии, что известен факт существования Е.
Согласно теореме Байеса
|
|
(7)
|
или, если было определено, что событие Е не наступило,
|
|
(8)
|
Примем, что для некоторого события Н существует большое число отдельных свидетельств, подтверждающих или не подтверждающих его, которые последовательно выясняются в процессе функционирования экспертной системы. Назовем их соответственно Е1, …, Еn. Если бы все они были выявлены одновременно и не зависели друг от друга, то можно было бы вычислить Р(Е: Н) как произведение отдельных вероятностей Р(Еi: Н), а затем вычислить Р(Н: Е), где Е – событие, состоящее в том, что “произошло осуществление всех Еi”. Аналогично мы определили бы Р(не Е: Н) как произведение всех Р(не Еi: Н).
Вместо этого обычно происходит поэтапное выяснение свидетельств. При этом происходит суммирование отдельных свидетельств и их влияний на условную вероятность по мере наступления отдельных Еi. Это можно сделать, используя априорные и апостериорные вероятности, следующим образом.
- Р(Н) – априорная вероятность события Н.
- Для данного свидетельства Еi запишем Р(Еi: Н) и Р(Еi: не Н).
- С учетом теоремы Байеса подсчитаем Р(Н: Еi) или Р(Н: не Еi) в зависимости от исхода Еi, т.е. вычислим апостериорную вероятность события Н.
- Теперь можно не обращать внимания на все наступившие Еi и переобозначить текущую апостериорную вероятность события Н как новую априорную вероятность Н. Итак, пусть Р(Н) равна Р(Н: Еi) или Р(Н: не Еi) в зависимости от значения Еi.
- Выберем новое свидетельство для рассмотрения
и перейдем
к п. 1.
На каждой итерации данного алгоритма формируются, так называемые, промежуточные выводы. Эти выводы, строго говоря, не всегда являются необходимыми, но они могут быть полезны для “очеловечивания” экспертной системы. Промежуточный вывод иногда используется в качестве входной переменной для другой ступени экспертной системы. Следует отметить, что наличие таких выводов существенно усложняет логику работы экспертной системы.
Однако есть один момент, который важно иметь в виду, рассматривая промежуточные выводы. Все зависит от такого важного вопроса, как независимость.
В большинстве статистических методов предполагается независимость различных свидетельств Еi, и часто такое предположение ничем не подтверждается.
Если существует n факторов (свидетельств), подтверждающих справедливость гипотезы Н, и они коррелированны друг с другом, а вычисления проделаны в предположении, что такой корреляции не существует, то гипотеза Н получит большую поддержку, чем этот факт сам по себе того заслуживает. Введение промежуточных выводов в процессе рассуждений может помочь исключить подобный эффект.
Рассмотрим события Е1 и Е2: они оба представлены в подтверждение гипотезы H1. пусть H1 – промежуточный вывод, действующий как свидетельство для дальнейшего вывода H2. Допустим также, что Е1 и Е2 коррелированны в какой-то степени между собой. Тогда H1 получит большую поддержку, чем нужно. Однако фактически ее все еще достаточно для того, чтобы считать гипотезу H1 истинной, следовательно, реального ущерба это пока не принесло.
Но без H1 ошибка в вычислении Е1 и Е2 перешла бы в H2, постепенно становясь все более и более серьезной по мере того, как в процессе вычислений добавляются возможно коррелированные Еi.
Присутствие H1 и других промежуточных выводов позволяет избавиться от накопленных ошибок. Для H2 следует начать новую последовательность вычислений, основанную на меньшем числе свидетельств, уменьшая тем самым риск формирования новой неопределенности.
Рассмотрим теперь проблему интерпретации откликов пользователя. Допустим, пользователь не очень уверен в ответе на какой-либо вопрос. Он, возможно, хотел бы ответить, ориентируясь на определенную шкалу, например от –5 до +5, где –5 означает “Нет”; 0 – “Не знаю”, а +5 – “Да”.
Представим теперь, что априорная вероятность любой реакции равна Р(Е).
Если есть неопределенность в ответе, то экспертная система должна использовать эту вероятность, взяв ее значение Р(Е), а также значение Р(не Е), так как если пользователь не уверен относительно существования конкретного свидетельства, то этого свидетельства, возможно, не существует.
Пусть Р – это отклик пользователя. Если Р ³ 0, то
|
|
(9)
|
если же Р < 0, то
|
|
(10)
|
Очевидно, что Р(не Е) = 1 – Р(Е), и при Р = 0 параметр Р(Е) остается неизменным. Тогда новое значение
|
|
(11)
|
Другими словами, вычисляются оба исхода, и взвешивается окончательный исход с учетом определенности, которую пользователь выразил как в пользу данного свидетельства, так и против него.
Отсюда видно, что модель Нейлора, реализованная с помощью теоремы Байеса, великолепно подходит для ситуаций, когда мнение эксперта построено на его опыте или интуиции. В отличие от этой модели, модель логики высказываний не позволяет с такой гибкостью учитывать интуицию и опыт эксперта; она больше похожа на модель, построенную не на знаниях и опыте эксперта, а на знаниях, полученных из учебников.
Логика высказываний – это формальная система, которую называют также пропозициональной логикой или исчислением высказываний. Логику высказываний относят к теоретическим моделям представления знаний логического направления искусственного интеллекта. Данное направление уделяет серьезное внимание генерации выводов на основе строгой последовательной системы, или иначе, формальной логики. Логика высказываний, как следует из термина, оперирует логическими высказываниями. При этом формально логическим высказываниям сопоставляются некоторые идентификаторы, а логическая обработка самих высказываний заменяется обработкой этих идентификаторов.
Логика высказываний может быть использована для решения задач, характеризующихся полнотой описания предметной области, то есть в тех случаях, когда есть возможность применить решающие правила.
Под решающими правилами понимаются правила следующего вида [2]:
Если A то B, где
А и В являются логическими выражениями.
В логическое выражение В в качестве операндов могут входить как свидетельства, так и гипотезы, а в логическое выражение А – только свидетельства.
В связи с тем, что разработанная система “Эксперт” задумывалась как опытный макет будущего программного комплекса, в систему решающих правил были введены следующие упрощения:
- логическое выражение В должно состоять только из одного операнда – гипотезы или свидетельства;
- в выражении А допустимо использовать следующие логические операции (операции перечислены сверху вниз в соответствии с убыванием их приоритета):
& – конъюнкция;
| – дизъюнкция.
Фреймовая модель в контексте системы “Эксперт” представляет собой множество фреймов. Фрейм – это информационная единица, отображающая шаг диалога в режиме выполнения экспертной системы. Фрейм состоит из текстовой и графической информации, выдаваемой на экран, и элементов управления, предназначенных для ввода пользователем информации в ответ на запросы системы. Фреймы в системе “Эксперт” могут содержать следующие визуальные компоненты:
- Текстовая вставка – используется для размещения на фрейме пояснительной и справочной информации. Разработчик может указывать параметры шрифта, оформления и начертания текста, его местоположение на форме, размеры области, в которой необходимо разместить текст, а также необходимость и содержание всплывающих подсказок, которые появляются при подведении указателя мышки к данному объекту.
- Поле ввода – используется для получения от пользователя ответов на задаваемые экспертной системой вопросы во время ее выполнения. Тип и диапазон допустимых для ввода значений задается типом вопроса. Разработчик может указывать параметры шрифта, оформления и начертания символов в поле ввода, его местоположение на форме, размеры, начальное значение (ответ пользователя по умолчанию), а также необходимость и содержание всплывающих подсказок, которые появляются при подведении указателя мышки к данному объекту.
- Переключатель (Check Box) – используется для получения от пользователя ответа, логического типа (“Да” или “Нет”). Разработчик может указывать параметры шрифта, оформления и начертания подписи к данному элементу управления, его местоположение на форме, размеры, начальное значение (значение по умолчанию), а также необходимость и содержание всплывающих подсказок, которые появляются при подведении указателя мышки к данному объекту.
- Элемент выбора (Radio Button) – используется для того, чтобы дать пользователю возможность выбрать ответ из нескольких вариантов. Если число вариантов равно двум, то целесообразно вместо этого элемента использовать переключатель. Разработчик может указывать параметры шрифта, оформления и начертания подписи к данному элементу управления, его местоположение на форме, размеры, начальное значение (значение по умолчанию), а также необходимость и содержание всплывающих подсказок, которые появляются при подведении указателя мышки к данному объекту.
- Картинка – используется для размещения на форме картинки. Разработчик, помимо самой картинки (в виде bmp-файла), может указывать ее размеры и местоположение на форме, необходимость автоматического определения ее размеров или автоматического растягивания, если ее размеры меньше заданных, а также необходимость и содержание всплывающих подсказок, которые появляются при подведении указателя мышки к данному объекту.
- Геометрическая Фигура – используется для размещения на форма геометрических фигур. Разработчик может разместить на форме следующие фигуры: Прямоугольник, прямоугольник с закругленными углами, квадрат, квадрат с закругленными углами, круг и эллипс. Помимо типа фигуры Вы можете указать цвет и стиль ее заливки и границы, а также необходимость и содержание всплывающих подсказок, которые появляются при подведении указателя мышки к данному объекту.
Таким образом, разработчику предоставляется достаточно средств для проектирования дружественного пользователю интерфейса.
Теперь пришло время немного остановиться и подвести некоторые итоги. Прежде всего, следует отметить что загадочное, и признаться, малопонятное словосочетание “Искусственный интеллект” на деле обернулось математически элементарно описываемой моделью, позволяющей без особых трудностей реализовать довольно сложные системы искусственного интеллекта – экспертные системы. Однако, решив только что описанными методами вопрос о моделях представления знаний, мы породили другую проблему – проблему извлечения и формализации знаний. В общем виде, модель разработки любой экспертной системы можно представить следующим образом (рис. 2).
 |
|
Рис. 2.
Модель разработки экспертной системы
|
Из рисунка видно, что формализацию знаний осуществляет не эксперт, а разработчик экспертной системы. Это связано с тем, что, как правило, эксперт не имеет достаточного объема знаний в области проектирования экспертных систем. На разработчика ложится сразу несколько задач. Во-первых, разработка самой экспертной системы (если он использует какую-нибудь среду для разработки экспертных систем, например “Эксперт”, то этот этап как таковой практически отсутствует). А, во-вторых, ему предстоит сложная задача работы с экспертом. Проблема состоит в том, что эксперт, обладая знаниями и навыками их применения, не всегда способен в четкой форме предоставить их разработчику. Поэтому разработчику необходимо потратить некоторое время для того, чтобы объяснить эксперту как он планирует организовывать работу системы, с тем, чтобы дать ему понять, какие его знания и в каком виде необходимы. На этом этапе очень важно четко сформулировать все задачи, которые должна решать разрабатываемая экспертная система.
На основании перечня задач необходимо сформировать перечень всех возможных исходов – экспертных оценок, к которым может прийти система в процессе работы. Эти исходы принято называть гипотезами. Если в этом списке не окажется какой-либо из гипотез, забытой экспертом (а такое обязательно будет), то в дальнейшем у разработчика может появиться печальная необходимость переделки системы. Как правило, подобные ситуации (желание эксперта добавить в систему новые гипотезы) возникают при первых демонстрациях и проверках правильности работы разработанной системы. Для того, чтобы избежать этого, рекомендуется перед непосредственно разработкой “проиграть” с экспертом сценарий работы системы на бумаге.
После того, как множество гипотез сформировано, необходимо определить множество фактов (свидетельств), являющихся факторами, влияющими на “победу” той или иной гипотезы. Как Вы уже убедились, многие методы, лежащие в основе моделей представления знаний в экспертных системах, строятся, исходя из предположения о независимости событий. На практике это означает, что качество работы экспертной системы снижается с увеличением зависимостей между ее свидетельствами.
Однако, несмотря на важность этих этапов, наиболее ответственной операцией является назначение логических связей между свидетельствами и гипотезами. Как мы уже говорили, под знаниями нужно понимать не только данные, но и алгоритмы их обработки. Условно можно сказать, что, задавая множество свидетельств и гипотез, мы определяем данные, а, задавая логические связки между ними, мы, фактически, задаем алгоритмы их обработки.
Теперь на примере создания прикладной экспертной системы в оболочке “Эксперт” давайте разберем все вышесказанное. В качестве примера, рассмотрим примитивную систему предсказания погоды, которая осуществляет прогноз погоды на завтрашний день, исходя из данных о погоде сегодня. Этот пример стал уже классическим для изучения экспертных систем.
В основу данной системы положим модель Нейлора. Для того чтобы создать новую экспертную систему в оболочке “Эксперт” выберите пункт “Создать новую ЭС…” в подменю “Файл” главного меню. На экране появится окно “Создание новой ЭС”, в котором расположены две пиктограммы: модель Нейлора и Логика высказываний. Так как в основу нашей системы мы решили положить нейлоровскую модель, то Вам необходимо щелкнуть мышкой по пиктограмме “Модель Нейлора” и нажмите кнопку “Применить”.
На экране появится окно, в котором необходимо указать каталог и имя файла для создаваемой экспертной системы, после чего нажать кнопку “Сохранить”.
Теперь, когда шаблон системы создан, необходимо формализацией знаний. Из-за простоты системы, нет необходимости привлекать постороннего эксперта, поэтому в качестве эксперта будем выступать непосредственно мы.
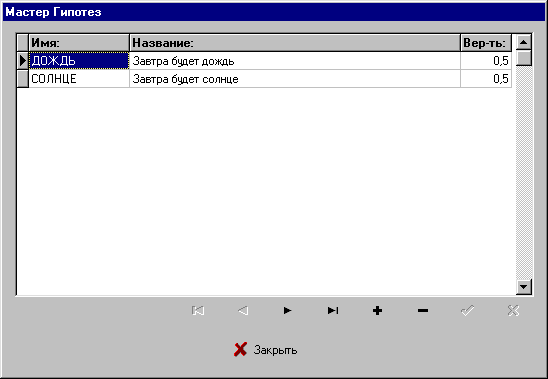
Итак, мы будем предсказывать погоду в мифической стране Умба-Юмба. На протяжении многих лет мы собирали статистику по погоде в этой стране, и сейчас, наконец, готовы к реализации экспертной системы. Множество гипотез в нашей системе будет крайне просто: “Дождь” и “Солнце”. Это означает, что система сможет предоставить нам две экспертные оценки: “Завтра будет дождливо” и “Завтра будет солнечно”. В стране Умба-Юмба количество дождливых дней в году равно количеству солнечных, поэтому априорные вероятности наших гипотез равны 0,5.
Для того, чтобы в системе “Эксперт” задать множество гипотез необходимо выбрать пункт “Гипотезы…” в подменю “Инструменты” главного меню. Заполните поля в появившейся на экране таблице как показано на рис. 3.
Так как мы изначально договорились, что будем предсказывать погоду на завтра исходя только из сегодняшней погоды, то нам потребуется всего два свидетельства: “Сухо”, означающее, что сегодня солнечная погода и “Сыро”, означающее, что сегодня идет дождь.
Для того, чтобы в системе “Эксперт” задать множество свидетельств необходимо проделать действия аналогичные тому, что Вы делали, задавая множество гипотез, только вместо пункта меню “Гипотезы…” Вам нужно выбрать пункт “Свидетельства”.
 |
|
Рис. 3.
Формирование множества гипотез
|
После того, как Вы определили множество гипотез и свидетельств, Вы получили полное представление о том, как будущая система будет работать. Поэтому на этом этапе следует заняться разработкой пользовательского интерфейса. Для этого выберите пункт “Фреймы…” в подменю “Инструменты” главного. На экране появится окно, состоящее из панели инструментов и пустой формы с закладками. Каждая закладка – это шаблон фрейма. Количество фреймов определяется количеством свидетельств, поэтому Вам потребуется создать два фрейма, на которых пользователю будут задаваться вопросы и один фрейм, если он Вам нужен, для заставки системы.
Теперь, раз возникла необходимость задавать пользователю вопросы, пришло время определить их перечень. Очевидно, нам нужно задать всего два вопроса: “Сегодня сухо?” и “Сегодня влажно?”. На первый взгляд может показаться, что надобности в двух вопросах нет, ведь, вроде бы, можно задать один из них, а на второй самостоятельно вычислить ответ, который будет равен логической инверсии ответа на первый вопрос. Однако это далеко не так. Как мы уже говорили, свидетельства должны быть независимыми, поэтому мы должны их рассматривать как независимые события. Кроме того, не надо забывать, что в один и тот же день возможно и солнце, и дождь (здесь мы не затрагиваем такое явление природы как “грибной дождик”).
Для того, чтобы ввести в нашу систему вопросы выберите пункт “Вопросы…” в подменю “Инструменты” главного меню. На экране появится “мастер Вопросов”, следуя рекомендациям которого вы сможете быстро задать все необходимые параметры вопросов. После того, как вопросы созданы, необходимо связать их со свидетельствами. Для этого необходимо вернуться в список свидетельств (Главное меню\Инструменты\Свидетельства…) и заполнить для каждого свидетельства самый правый столбец, в котором необходимо выбрать из выпадающего списка соответствующий данному свидетельству вопрос.
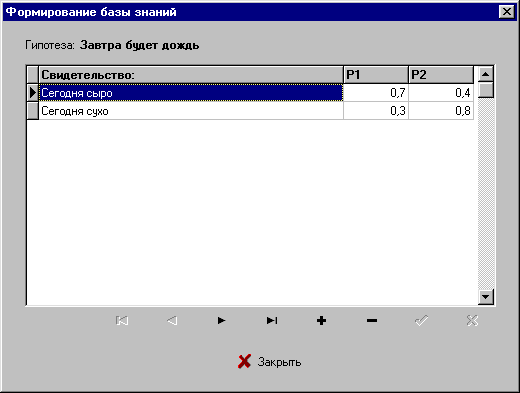
Теперь для того, чтобы система заработала необходимо задать связи между свидетельствами и гипотезами, то есть определить параметры обработки информации. Для ввода этих связей предусмотрена специальная форма “Формирование базы знаний”, показанная ниже:
 |
|
Рис. 4.
Форма формирования ядра экспертной системы
|
Данная форма вызывается для каждой гипотезы (для этого нужно дважды щелкнуть мышкой по имени соответствующей гипотезы в главном окне программы) и представляет собой таблицу, в которой каждому свидетельству ставится в соответствие две условных вероятности: вероятность данного свидетельства при правильности данной гипотезы (Р1) и вероятность данного свидетельства при ложности данной гипотезы (Р2).
Предположим, что на основании многолетней статистики погоды, мы получили следующие значения:
Для гипотезы “ДОЖДЬ”:
(Сегодня сыро, 0.7, 0.4).
(Сегодня сухо, 0.3, 0.8).
Для гипотезы “СОЛНЦЕ”:
(Сегодня сыро, 0.2, 0.7).
(Сегодня сухо, 0.8, 0.4).
На этом мы закончили разработку системы предсказания погоды. Теперь Вы можем запустить только что созданную экспертную систему и проанализировать ее работу. Для запуска системы нажмите кнопку “Начать”, расположенную на панели инструментов (кнопка имеет иконку в виде красного треугольника). Предположим, что сегодня “Не влажно” и “Сухо”. Тогда наша система выдвинет следующую экспертную оценку:
Завтра будет дождь с вероятностью 0,158
Завтра будет солнце с вероятностью 0,842
Теперь интересно будет проследить, как оно пришла к такому решению. Для этого введем следующие обозначения:
Р(Д)i – вероятность дождя на i-том шаге итерации.
Р(С)i – вероятность солнца на i-том шаге итерации.
P(A:B) – вероятность события А при существовании события В.
Р(Сыро) = 0 (из-за того что мы отметили, что сегодня “не Сыро”).
Р(Сухо) = 1 (из-за того что мы отметили, что сегодня “Сухо”).
В этих обозначениях работа нашей систем выглядит так:
Р(Д: Сыро)1 =
Р(Сыро: Д)*P(Д)0/(Р(Сыро:
Д)*Р(Д)0 + Р(Сыро:не Д)*
*Р(не Д)0) = 0.7*0.5/(0.7*0.5 + 0.4*0.5)=0.46(6)
Р(Д: не Сыро)1=
Р(не Сыро: Д) * P(Д)0/(Р(не
Сыро: Д)*Р(Д)0 +
+Р(не Сыро: не Д)*Р(не Д)0)= 0.3*0.5/(0.3*0.5 + 0.6
* 0.5) = 0.33(3)
Р(Д)1= Р(Д: Сыро)1*Р(Сыро) + Р(Д: не Сыро)1*Р(не Сыро) = =0.46(6)*0+0.33(3)*1 = 0.33(3)
Р(С: Сыро)1=Р(Сыро:
С)*P(С)0/(Р(Сыро: С)*Р(С)0
+ Р(Сыро: не С)*
*Р(не С)0)= 0.2*0.5/(0.2*0.5 + 0.7*0.5)= 0.22(2)
Р(С: не Сыро)1=
Р(не Сыро: С) *P(С)0/(Р(не
Сыро: С)*Р(С)0 +
+Р(не Сыро: не С)*Р(не С)0) = 0.8*0.5/(0.8*0.5 + 0.3*0.5)=
0.72(72)
Р(С)1=
Р(С: Сыро)1*Р(Сыро)+ Р(С:
не Сыро)1*Р(не Сыро)=
=0.22(2)*0+0.72(72)*1= 0.72(72)
Р(Д: Сухо)2=Р(Сухо:
Д)*P(Д)1/(Р(Сухо: Д)*Р(Д)1
+
+Р(Сухо: не Д)*Р(не Д)1)= 0.3*0.33 / (0.3*0.33 + 0.8*
0.66)= 0.158
Р(Д: не Сухо)2=
Р(не Сухо: Д) * P(Д)1/(Р(не
Сухо: Д)*Р(Д)1 +
+Р(не Сухо: не Д)*Р(не Д)1)= 0.7*0.33/(0.7*0.33 + 0.2
* 0.66) = 0.63(63)
Р(Д)2=
Р(Д: Сухо)2*Р(Сухо)+ Р(Д:
не Сухо)2*Р(не Сухо)=
= 0.158*1+0.63(63)*0= 0.158
Р(С: Сухо)2=Р(Сухо:
С)*P(С)0/(Р(Сухо: С)*Р(С)0
+ Р(Сухо: не С)*
*Р(не С)0)= 0.8*0.72(72)/ (0.8*0.72(72) + 0.4*0.27(27))=
0.842
Р(С: не Сухо)2=
Р(не Сухо: С) *P(С)0/(Р(не
Сухо: С)*Р(С)0 +
+Р(не Сухо: не С)*Р(не С)0)= 0.2*0.72/(0.2*0.72 + 0.6*0.27)=0.47
Р(С)2= Р(С: Сухо)1*Р(Сухо) + Р(С: не Сухо)1*Р(не Сухо)= =0.842*1+0.47*0= 0.842
На этих страницах я попытался кратко осветить свою личную позицию по некоторым вопросам проектирования экспертных систем, показать, что в основе многих разделов теории искусственного интеллекта лежат замечательно простые и в тоже время необычайно мощные математические модели. Весь путь мыслей, сомнений, догадок и разработок, изложенный в этой статье мне не так давно довелось пройти самому. И если мой опыт пробудит в ком-нибудь интерес к этой области и подвигнет к созданию чего-нибудь нового и интересного, то тогда, можно будет считать, что мои усилия не пропали даром.
Литература
| Кузин, 1989 | Кузин Е.С., Ройтман А.И., Фоминых И.Б., Хахалин Г.К., Интеллектуализация ЭВМ – М.: Высшая школа, 1989. |
| Нейлор, 1991 | Нейлор К., Как построить свою экспертную систему – М.: Энергоиздат, 1991. |
| Трахтенгерц, 1998 | Трахтенгерц Э.А., Компьютерная поддержка принятия решений – М.: Синтег, 1998. |