М.Ю. Кадакин

Распознавание шифров источников Рукописной древнерусской картотеки XI–XVII вв.

В данной статье рассматриваются вопросы, связанные с распознаванием рукописного текста. Ниже приведенные методы и алгоритмы составляют основу математической модели при распознавании рукописных фраз ограниченного словаря. Все ниже изложенное разрабатывалось с целью применения в распознавании карточек Рукописной древнерусской картотеки, хранящейся в Институте русского языка им В.В.Виноградова РАН, для создания электронной картотеки. Картотека состоит из 1.5 миллионов карточек, содержащих выписки более чем из трех тысяч источников - древнерусских памятников письменности ХI–XVIII веков. В статье представлены разработки выполненные автором в рамках дипломного проекта седьмого курса на кафедре "Автоматизированные системы обработки информации и управления" МГТУ им. Н.Э.Баумана, руководитель проекта к.т.н., доц. Ю.Н.Филиппович

Структура типичной карточки Рукописной древнерусской картотеки представлена на рис 1.

Задача перевода Картотеки в электронный вид усложняется тем, что составлением данной картотеки занималось порядка 200 человек и, следовательно, в картотеке присутствует такое же число различных почерков.

Для определения принадлежности текста конкретному почерку используется тот факт, что при составлении картотеки каждый источник расписывал, как правило, один человек. Исходя из данного факта, задача определения почерка сводится к задаче распознавания шифра источника, представленного на карточке.

Метод распознавания на основе внешних признаков изображения.

В связи с тем, что заранее принадлежность текста карточки какому-либо почерку считалась неизвестной, распознавание шифра источника затруднено. В этом случае основная проблема распознавания связана с сегментацией рукописной строки на символы. При реализации сегментации изображения на символы, полученная эффективность разбиения не превысила 50% (т.е. из всех сегментированных изображений менее половины представляло собой действительно отдельные символы).

Для распознавания шифра источника было принято решение отказаться от сегментации изображения на символы и распознавать его по “внешнему виду”. В качестве параметров “внешнего вида” используются число слов и наличие знаков препинания (под “словом” здесь и далее будем понимать любую последовательность букв и цифр, входящую в шифр источника и обособленную от других “слов” знаками препинания либо символами пробела). Для каждого слова определяется число букв в нем, а также наличие выступающих элементов в верхней и нижней частях строк, и их относительное положение в слове.

В рассматриваемом случае число возможных шифров источников было равно 3949. Было произведено предварительное исследование эффективности распознавания шифров источников по внешним признакам, перечисленным выше. Целью данного исследования было определение вероятности корректного распознавания шифра источника без дополнительных вычислений и преобразований.

В процессе исследования, брался текст очередного шифра источника, и его признаки (число слов, наличие знаков препинания, число букв в слове, наличие выступающих элементов в слове и их местоположение) сравнивались с признаками остальных шифров источников. При отсутствии других шифров источников с такими же признаками считалось, что данный шифр источника однозначно определяется по внешним признакам. Результаты исследования приведены в столбце “А” таблицы 1.

Из полученных данных следует, что только 66% от всех шифров источников можно однозначно определить по внешним признакам, приведенным выше.

Проанализировав различные варианты шифров источников, можно заметить, что 606 из них содержат римские цифры. Задача распознавания римских цифр намного легче задачи распознавания рукописного текста. Введя поправку на возможность распознания римских цифр, входящих в шифр источника, получим уточненные данные (см. столбец “Б” табл. 1).

С учетом внесенной поправки на распознавание римских цифр, получаем, что 73% от всех шифров источников однозначно определяются по определенным выше признакам, а 92% от всех шифров источников имеют не более 4 совпадений по признакам с остальными шифрами источников.

Вычислим вероятность определения шифра источника по внешним признакам Р_оши, будем считать, что все шифры источников равномерно распределены по карточкам картотеки:

Роши 0.8.

То есть мы получили, что вероятность определения шифра источника в карточке по внешним признакам без дополнительного распознавания равняется 0.8.

При анализе списка шифров источников было выяснено, что 969 всех шифров источников содержат хотя бы одно слово, состоящее из одной буквы. Следовательно, данное слово не надо сегментировать на буквы, а можно сразу попытаться распознать. С учетом сказанного были получены уточненные данные (см. столбец “В” табл. 1).

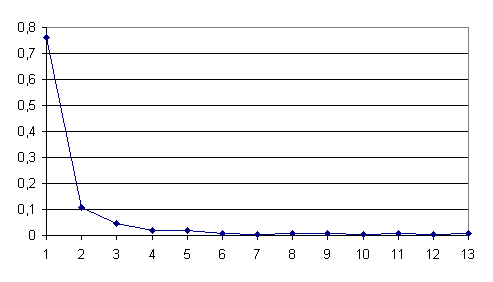
Уточненная функция распределения числа совпадений внешних признаков шифров источников представлена на рис. 2.

После внесения очередной поправки, получаем, что 75% от всех шифров источников однозначно определяются по внешним признакам, с учетом распознавания однобуквенных слов и римских цифр, а 94% от всех шифров источников имеют не более 4 совпадений по признакам с остальными шифрами источников.

Уточним вероятность определения шифра источника по внешним признакам Р_оши:

Роши 0.84.

В итоге мы получили, что уточненная вероятность определения шифра источника в карточке по внешним признакам, с учетом распознавания однобуквенных слов и римских цифр, без дополнительного сегментирования, равняется 0.84.

Реализация метода распознавания шифра источника.

Распознавание шифра источника представляет собой последовательное решение следующих задач (рис. 3), в которых определяются: границы изображения шифра источника, угол наклона строки, число слов в строке, верхняя и нижняя границы числа букв в слове, выступающие элементы, соответствие изображения конкретному шифру источника.

Определение границ изображения шифра источника. Описание этой задачи в статье не приводится, но в дальнейшем будем считать, что мы имеем дело с обработанным изображением шифра источника, т.е. с уже установленными в процессе обработки границами.

Определение угла наклона слова осуществлялось по следующему алгоритму: сначала выделялась область строки, располагающаяся в районе нижней границы строчных букв, в полученной области определялись точки локального минимума. Затем через полученные точки проводилась прямая по методу наименьших квадратов. Угол наклона данной прямой считался углом наклона слова и под ним в слове проводились верхняя и нижняя границы строчных букв.

Алгоритм определения числа слов в строке основан на разбиении всей строки на всевозможные фрагменты, вычислении расстояния между ними, а затем принятии решение о слиянии их в одно слово, либо о принадлежности данных фрагментов различным словам строки.

Побочным результатом работы алгоритма разбиения строки на слова является определение знаков препинания, входящих в строку. В качестве признака знака препинания (точки или запятой) берутся размеры фрагмента и его расположение в строке (для знаков препинания – вблизи нижней границы строчных букв).

Также при сегментации изображения на слова определяется наличие в шифре источника римских цифр. Основным признаком вхождения римских цифр в шифр источника является наличие горизонтальных линий в верхней и нижней областях строки.

Для определения числа слов в строке были использованы два различных метода, дающих соответственно верхнюю и нижнюю оценки числа букв в слове.

Алгоритм определения верхней границы числа букв в слове основан на определении числа точек локального минимума в нижней части изображения слова.

В ходе проведенных исследований было получено соотношение для определения верхней границы числа букв в слове:

, где: х – число букв в слове; N – число локальных минимумов.

Алгоритм определения нижней границы числа букв в слове основан на подсчете числа пересечений средней линии строки с изображением текста (рис. 5.). Соотношение для определения нижней границы числа букв в слове, полученное в результате проведенных исследований, выглядит следующим образом:

, где: х – число букв в слове, n – число пересечений изображения слова со средней линией.

Алгоритм определения выступающих элементов, относительно границ строчных букв основывается на нахождении элементов текста, не принадлежащих границам строчных букв и определении относительного местоположения данного элемента в слове.

Основные трудности, возникшие при реализации данного алгоритма были связаны с тем, что слова в строке шифра источника расположены под различными углами, вследствие чего границы строчных букв в слове определялись некорректно, что приводило к утере выступающих элементов или появлению новых, реально не существующих (рис. 6.).

Определение соответствия изображения конкретному шифру источника разбивается на несколько задач.

Каждая i-ая задача соответствует i-му сегментированному слову изображения строки и выявляет подмножество из всего множества шифров источников, для которого признаки i-ого слова соответствуют признакам i-го сегментированного слова.

Затем все полученные подмножества пересекаются. Если в конце обработки подмножеств остается одна строка шифра источника, то считается, что распознаваемая карточка принадлежит данному шифру источника.

Если же в результате пересечения подмножеств получится пустое множество, то результирующим подмножеством будет считаться подмножество, состоящее из шифров источников, входящих в наибольшее число первоначальных подмножеств.

В случае, когда результирующее подмножество содержит более одного шифра источника, для дальнейшего распознавания требуется дополнительный анализ изображения, например попытка распознать римские цифры или однобуквенные слова в шифре источника.

В случае если и после дополнительного анализа подмножество возможных результатов содержит более одного шифра источника, используется анализ выступающих элементов. При анализе нижних выступающих элементов, все возможные элементы разбиваются на три группы: “большая петля” - для букв ‘у’ и ’д’, “малая петля” - для букв ‘щ’ и ‘ц’ и “линия” - для буквы ‘р’.