
При анализе и обработке растровых изображений часто возникает необходимость работать с изображением не как с массивом точек, а как с набором команд, описывающих это изображение (например, чертежи, карты и т. д.). Проблема перевода растровых изображений в векторный формат возникает также при построении систем распознавания графических образов. В самом простом случае это можно проиллюстрировать следующим примером: дан массив точек (растровое изображение), на котором предположительно есть некоторый треугольник. Необходимо проверить наличие данного объекта в этом массиве. Задача, согласитесь, намного упростится, если то же изображение будет задано тремя командами line: line(x1_i, y1_i, x2_i, y2_i), i=1, 2, 3.
В данной статье рассматривается алгоритм векторизации растровых изображений (256 цветов; градации серого – GrayScale). Изображение может содержать полутоновые переходы и элементы с расплывчатыми границами. Процесс векторизации можно условно представить в виде последовательности пяти этапов (рис. 1).
Рассмотрим эти этапы более подробно. В дальнейших рассуждениях некоторые понятия заключаются в кавычки из-за условности их применения в изложении обобщенных принципов работ алгоритмов.
Растровое изображение (с палитрой из 256-ти цветов) строится приблизительно следующим образом: элементы массива размером X_size*Y_size*sizeof(char)= X_size*Y_size байт после распаковки графических данных из файла содержат номера цветов в палитре. Каждый элемент массива лежит в пределе [0, 255] и соответствует одному пикселю.
В палитре хранятся R-, G- и B- составляющие цветов, используемых в изображении. N-му номеру цвета соответствует N-ая тройка байтов в палитре.
Для дальнейших рассуждений примем некоторые соглашения по формату входных данных:
 |
|
Рис. 1. Этапы векторизации
|
Используются изображения с палитрой (256 цветов) GrayScale (градации серого). Это подразумевает: что R-, G- и B – составляющие цветов в палитре равны; каждой составляющей отводится по 1 байту, то есть значение каждой составляющей цвета в палитре изменяется в пределах [0,255]; первая тройка байтов в палитре соответствует черному цвету, последняя – белому; в палитре цвет «плавно» изменяется от черного к белому. Получаем палитру следующего вида:
00h 00h 00h 01h 01h 01h 02h 02h 02h 03h 03h 03h........feh feh feh ffh ffh ffh (всего: 256*3*1=768 байт).
Эти условия выполняются при конвертировании в формат GrayScale(8 бит) большинством конвертеров, например, конвертером, включенным в MS Photo Editor.
Итак, после распаковки растрового файла создается массив размером X_size*Y_size*sizeof(char)= X_size*Y_size, содержащий номера цветов из палитры ([0. 255]).
Для неточной обработки с целью упрощения вычислений интенсивность можно округлять до ближайшего целого числа, кратного 16. Но этот частный случай здесь не рассматривается.
Если до этого подразумевались целочисленные величины (номера цветов), то теперь переходим к использованию дробных чисел для описания пикселей. Мы можем сделать это, поскольку при равномерном изменении цветов в палитре нас уже не интересуют сами номера цветов в палитре. Нам, например, достаточно знать, что пиксель, которому поставлено в соответствие число 55.5, «светлее» пикселя, которому соответствует число 55.0, и «темнее» пикселя, которому соответствует число 56.0. Дальше в рассуждениях термины «цвет» и «интенсивность» можно считать равноценными.
В целях устранения мелких неровностей (шумов) в изображении и установки нужной при анализе чувствительности проводится усреднение цвета: замена цвета пикселя средним цветом его окружения.
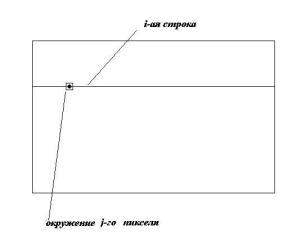
Для каждой строки изображения перебираются пиксели, и для каждого пикселя вычисляется и запоминается, например, в одномерном массиве среднее значение цвета в квадрате вокруг него (рис. 2). Размер квадрата является одним из входных параметров при выделении границ. Чем больше квадрат, тем меньше чувствительность к маленьким элементам (дефектам) изображения и тем меньше колебания в цвете от пикселя к пикселю. (В программной реализации этот параметр мог находиться на отрезке [1, 6]).
Итак, для i-ой строки мы уже имеем одномерный массив, в котором номер элемента является номером пикселя в строке, а значением элемента является средний цвет его окружения. В этом массиве выделяем участки возрастания и убывания интенсивности (рис. 3). Возрастание или убывание не обязательно должны быть строгими: допускается содержание в них некоторых «небольших» участков с нулевым (или даже с «небольшим» обратным) изменением интенсивности. Также следует отметить тот факт, что участки монотонности могут быть «достаточно длинными», поэтому необходимо ограничивать максимальную длину участков.
Теперь для выделенного участка каждому пикселю ставим в соответствие разницу в цвете между ним и следующим за ним пикселем. Назовем эту разницу весом; чем больше разница в интенсивности между соседними пикселями, тем больший вес (или значение) имеет пиксель.
 |
|
Рис. 2. Замена интенсивности пикселя средней интенсивностью
его окружения
|
 |
|
Рис. 3. Выделение участков возрастания и убывания.
Вычисление центра
|
Вычисление середины участка с учетом неравномерного изменения интенсивности проведем по следующей формуле:
 ,
, |
где ![]() – середина участка с учетом изменения интенсивности,
– середина участка с учетом изменения интенсивности, ![]() – расстояние i-ой точки от начала участка,
– расстояние i-ой точки от начала участка, ![]() – вес i–ой точки, а
– вес i–ой точки, а ![]() – разница в интенсивности между последним и первым пикселями участка.
При этом, необходимо учесть, что
– разница в интенсивности между последним и первым пикселями участка.
При этом, необходимо учесть, что ![]() должна лежать в определенном отрезке значений, задаваемом как входной
параметр для процедуры (подобно размеру окрестности при усреднении интенсивности).
Если
должна лежать в определенном отрезке значений, задаваемом как входной
параметр для процедуры (подобно размеру окрестности при усреднении интенсивности).
Если ![]() не входит в этот отрезок значений, то данный участок возрастания (убывания)
игнорируется. Для удобства можно перейти к относительным координатам, взяв за
начало участка ноль. При этом суммирование ведется от нуля до конца участка.
Эта формула не учитывает различия в восприятии человеком цветов разных интенсивностей,
обусловленные особенностями зрительного аппарата человека. Эта поправка незначительна
по сравнению с погрешностями при вычислениях, так что ею можно пренебречь.
не входит в этот отрезок значений, то данный участок возрастания (убывания)
игнорируется. Для удобства можно перейти к относительным координатам, взяв за
начало участка ноль. При этом суммирование ведется от нуля до конца участка.
Эта формула не учитывает различия в восприятии человеком цветов разных интенсивностей,
обусловленные особенностями зрительного аппарата человека. Эта поправка незначительна
по сравнению с погрешностями при вычислениях, так что ею можно пренебречь.
Чтобы «тонкие» линии заменять одной линией посередине, а не двумя – ее контурами, проверяются расстояния между серединами соседних участков, и если они «достаточно близки», то две соседние точки заменяются одной – посередине между ними.
Горизонтальные, или «почти горизонтальные» линии на изображении не будут выделены при анализе только по строкам. Поэтому, после того, как изображение будет проанализировано по строкам, оно анализируется аналогичным образом по столбцам.
Полученный растровый образ контуров в ходе анализа запоминается в двумерном массиве. Теперь мы можем работать с двухцветным изображением.
Для самого процесса векторизации производится последовательный перебор пикселей в двумерном массиве, и, если встречается пиксель контура, то запускается процедура выделения отдельного связного контура. При поиске контур запоминается как отдельный объект, и после окончания поиска стирается из массива контуров и передается в процедуру векторизации. Подобная последовательность действий осуществляется для остальных необработанных контуров.
Записывать координаты можно в одномерный массив, в котором номер ячейки представляет собой координату по оси абсцисс, а его содержимое – координату по оси ординат. Однако, этот метод не является эффективным, поскольку при этом невозможно запомнить координаты замкнутых контуров и линий, представляющих собой многозначные функции. Кроме того, в дальнейшей работе будут проявляться неточности при усреднении и интерполяции участков с почти прямым углом наклона к оси абсцисс. Поэтому, не будем останавливаться на этом методе подробно и рассмотрим другой, более интересный, и лишенный тех недостатков, которые имел предыдущий метод. Суть его заключается в том, что при поиске координаты запоминаются в двух одномерных массивах: в одном массиве запоминаются координаты по оси абсцисс, в другой – координаты по оси ординат. Здесь функция всегда однозначна, и с ней легче работать. По сути, мы имеем параметрическое описание последовательности точек, составляющих контур. Здесь параметром является номер точки. При этом, нам, в отличие от предыдущего метода, придется следить за размером массивов, так как здесь мы заранее не знаем длину выделяемой линии. Еще один недостаток состоит в том, что нам при векторизации придется следить за точностью в интерполяции более строго, поскольку здесь мы будем интерполировать две последовательности точек: x(n), y(n) (n – параметр ). В этом случае одна интерполированная последовательность будет независимо от другой вносить свои ошибки.
Итак, рассмотрим алгоритм процедуры поиска. На входе мы имеем координаты точки на контуре, который необходимо выделить и запомнить из двумерного массива контуров. Задача состоит в том, чтобы выделить гладкую кривую, даже при условии, что она может быть пересечена другими кривыми, и иметь разрывы.
В начале поиска анализируется окружение этой точки, и если в окрестности найдена другая точка, то координаты старой точки запоминаются, она стирается из входного двумерного массива, и поиск точки в окрестности переходит в новую позицию. Размер окрестности задается разработчиком в зависимости от того, для какого класса точности изображений проектируется конкретная программа (обычно, это – 5-10 пикселей). После того, как будет найдено порядка 10-15 пикселей, можно делать оценку в направлении поиска точек по «первой производной», то есть, путем проведения прямой через усредненные начальную и конечную точки (рис. 4). После того, как будет найдено порядка 50 пикселей, если это требуется, можно также сделать оценку направления поиска по «второй производной» (выпуклость, вогнутость): либо провести ломаную прямую, либо использовать интерполяционный многочлен, и на его основе определить направление поиска, либо через три (усредненные начальную, среднюю и конечную) точки из уже найденных провести дугу окружности, и сделать оценку на его основе (рис. 5). Оценка проводится отдельно для обеих параметрически заданных переменных. Нужно отметить, что способ оценки, использующий полиномы, чувствителен к неровностям на контуре, и он может давать ошибки.
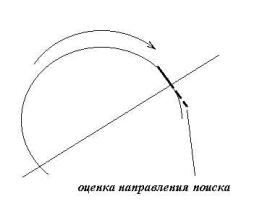 |
|
Рис. 4. Оценка направления поиска по «первой производной»
|
 |
|
Рис. 5. Оценка по «второй производной»: а) контур,
выделенный до указанной точки; б) оценка ломаной прямой; в) оценка полиномом;
г) оценка дугой. Штриховыми линиями указаны оценки направления поиска |
Сделав оценку, мы проверяем существование в окрестности предполагаемой линии, если она есть, то запоминаем ее и продолжаем поиск, если нет – то поиск прекращаем. Изначально могло так получиться, что мы начали поиск не с начала некоторой незамкнутой линии, а с какой либо другой точки. В этом случае мы должны вернуться в ту точку, с которой был начат поиск, и продолжить его снова (рис. 6). При этом будет выделена остальная часть линии. Следует учесть в этом случае необходимость сортировки точек с целью получения «непрерывной цепной» линии. При поиске возможны некоторые разрывы в линиях, для этого необходимо оставлять незаполненные ячейки в массивах для дальнейшего их заполнения отрезками прямых либо дугами.
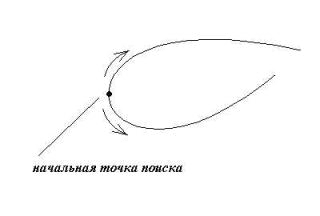 |
|
Рис. 6. Повтор поиска из начальной точки
|
Получив контур как отдельный объект, необходимо усреднить значения координат. Далее проводится интерполяция участков «плавных» кривых с целью получения значений координат между пикселями (с определенным шагом), а также для устранения неровностей. Ясно, что размер массивов будет увеличен. Интерполяцию лучше провести многочленами третьей степени (4 неизвестных – 4 степени свободы) либо сплайнами.
Теперь рассмотрим сам процесс векторизации.
На входе мы имеем два массива координат (x(n), y(n)) точек на контуре. Задача состоит в том, чтобы заменить их дугами и отрезками прямых.
Для начала отметим, что, так как здесь используются интерполированные значения координат, то случайные ошибки (неровности, угловатости и т. д.) исключены, поэтому для упрощенного учета ошибок достаточно просто установить порог (максимальное расстояние от точки дуги или прямой до точки контура, при котором мы считаем их совпадающими). Подобный подход дает вполне удовлетворительные результаты.
Радиус кривизны в точке можно вычислить по второй производной ( «Краткий курс по математическому анализу» Пискунов С.), и далее проводить дугу с вычисленным радиусом до тех пор, пока приближение дугой остается в заданных пределах. Однако, подобный способ очень чувствителен к погрешностям, тем более, что мы имеем дело с дискретными значениями координат.
Процесс векторизации удобнее провести непосредственным сравнением дуг и прямых с координатами точек контуров. Алгоритм выглядит следующим образом:
начальная_точка = Начальная точка.
конечная_точка = Конечная точка.
Конечная_точка, средняя_точка и начальная_точка лежат на одной прямой?
Да. Координаты точек между ними лежат на одной прямой (с заданной точностью)?
Да. Между ними прямая. Запомнить ее.
Начальная_точка=конечная_точка.
Конечная_точка=конечная точка.
Начать сравнение сначала с новыми переменными.
Нет. конечная_точка= конечная_точка - шаг. Продолжить сравнение.
Нет. Координаты точек между ними лежат на дуге (с заданной точностью)?
Да. Между ними дуга. Запомнить ее.
Начальная_точка= конечная_точка.
Конечная_точка=конечная точка.
Начать сравнение сначала с новыми переменными.
Нет. конечная_точка= конечная_точка - шаг. Продолжить сравнение.
Необходимо рассмотреть некоторые частные случаи, например, случай, при котором начальная и конечная точки оказываются в «непосредственной близости» друг от друга (в пространстве XY), и как следствие мы имеем большие погрешности при вычислении радиуса и центра окружности. Здесь просто можно временно взять другие точки.
В понятие «точка» мы вкладываем усредненное значение ее окружения.
Приведенные здесь алгоритмы были реализованы программно
в среде Borland C++ 5.01. При этом, были выбраны следующие
форматы данных: формат входных данных –PCX, выходных –DXF. Программа называется RASP, занимает ![]() 100
КВ дискового пространства.
100
КВ дискового пространства.
Подытожим эту статью. В результате проведенных вычислений и исследований была предложена схема векторизации растровых изображений. Были предложены несколько методов решения задач, возникших при разработке алгоритма. Были даны предварительные оценки этим методам, а также были отмечены некоторые их преимущества и недостатки.