Статистический анализ показателей
функционирования финансовых систем

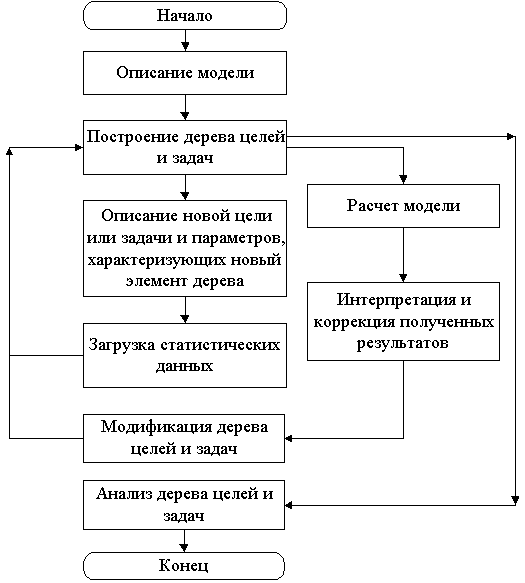
Для анализа деятельности и принятия решений о приоритетных направлениях развития сложных финансово-технических систем часто используется дерево целей и задач. Дерево объединяет в себе основную цель функционирования системы и иерархическую структуру частных целей и задач, решение которых необходимо для достижения основной цели.

Для корректного построения такого дерева лицу, принимающему решения, или эксперту необходимо подробно структурировать множество возможных показателей, определяющих эффективность функционирования всей системы, требуется также учитывать их соподчиненность, и разграничивать общие и частные цели и задачи. Решение проблемы структурирования возможно при тщательном анализе показателей — характеристик.

Общее число показателей может быть достаточно велико — от нескольких десятков до нескольких сотен. Каждая группа может состоять из нескольких факторов и результирующих характеристик. В общем случае группа может иметь непустое пересечение с другими объединениями. На основе полученного разбиения возможно построение иерархической системы показателей, используемых для построения дерева целей и задач.

Будем считать, что существующую статистическую информацию о функционировании системы можно представить в виде упорядоченного множества многомерных наблюдений:

,

(1)

Каждое наблюдение X_i можно представить в следующем виде:

,

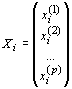(2)

— значение j-го показателя за i-й промежуток времени.

Основной задачей является переход от описания изучаемой системы, заданного большим набором непосредственно измеряемых показателей, к описанию меньшим числом максимально информативных признаков, отражающих наиболее существенные свойства системы.

Задача перехода (с наименьшими потерями в информативности) к новому набору признаков может быть описана [Ефимова, 1996] следующим образом.

Пусть Z = Z(X) — некоторая p-мерная вектор-функция исходных переменных x⁽¹⁾, x⁽²⁾, ..., x^(p) (p*<<p) и пусть I_p*(Z(X)) — определенным образом заданная мера информативности p^*-мерной системы признаков Z(X)=(z⁽¹⁾(x), z⁽²⁾(x), ..., z^(p*)(x)). Конкретный выбор функционала I_p*(Z) зависит от специфики реально решаемой задачи и опирается на один из возможных критериев: критерий автоинформативности (АИ), нацеленный на максимальное сохранение информации, содержащейся в исходном массиве {X_i}, i=1..n относительно самих исходных признаков, и критерий внешней информативности (ВИ), нацеленный на максимальное “выжимание” информации, содержащейся в исходном массиве {X_i}, i=1..n относительно некоторых других (внешних) показателей.

Задача заключается в определении такого набора признаков , найденного в классе F допустимых преобразований исходных показателей x⁽¹⁾, x⁽²⁾, ..., x^(p), что

.

(3)

При формировании такой системы признаков к последним предъявляются разного рода требования, такие как наибольшая информативность, взаимная некоррелированность и т.п. Имеется три основных вида предпосылок, обуславливающих возможность перехода от большего числа исходных показателей состояния (поведения) анализируемой системы к существенно меньшему числу наиболее информативных переменных.

1. Дублирование информации, доставляемой сильно взаимосвязанными признаками.
2. Неинформативность признаков, мало меняющихся от одного объекта (временного интервала) к другому.
3. Возможность агрегирования, т.е. простого или взвешенного суммирования по некоторым признакам.

Тот или иной вариант рассмотрения такой остановки задачи приводит к конкретному методу снижения размерности.

Рассмотрим некоторые виды методов снижения размерности. Некоторые сравнительные характеристики этих методов приведены в
табл. 1.

Характеристики	Методика
	Кластерный анализ. Теория автоматической классификации		Модель регрессионного анализа	Факторный анализ. Метод главных компонент
1	2		3	4
Основная цель	Разбиение на непересекающиеся множества, удовлетворяющие некоторому критерию однородности		Выбор наиболее информативных характеристик, описывающих объект	Выявление групп взаимозависимых параметров, изменяющихся во времени
Объекты исследования	Однородные объекты		Параметры — характеристики объекта	Параметры — характеристики объекта
Информативность	АИ	ВИ		АИ
Критерий качества	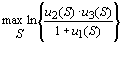, u1—среднее расстояние в классах, u2—степень удаленности классов, u3—степень одинаковости распределения наблюдений внутри класса	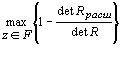, Rрасш—расширенная корреляционная матрица признаков, R—корреляционная матрица признаков
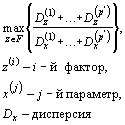Форма представления исходной информации	Матрица коэффициентов взаимной близости объектов	Множество статистических рядов динамики		Множество статистических рядов динамики
Используемые алгоритмы	Различные кластер-процедуры и объекты	Метод наименьших квадратов, метод максимального правдоподобия		Алгоритмы нахождения собственных чисел и векторов

Если число признаков невелико, взаимосвязи между ними могут быть хорошо представлены с помощью методов корреляционного и регрессионного анализа. Однако при большом числе признаков корреляционные модели малоэффективны и чересчур громоздки [Жуковская, 1976], тогда как модели факторного анализа во многих случаях позволяют без существенных потерь в информации представить большую систему признаков (несколько десятков) в компактном виде.

Основное предположение факторного анализа состоит в следующем: показатели исследуемой системы могут быть описаны в терминах небольшого числа основополагающих внутренних параметров — общих факторов.

Предполагается, что каждый из параметров x_j, описывающих систему, может быть представлен как функция небольшого числа общих факторов Z₁, Z₂, ..., Z_m и характерного фактора U_i :

Каждый общий фактор Z_j (i=1..m) имеет существенное значение для анализа всех переменных x_i (i=1..p). Изменение фактора U_i приводит к изменению только соответствующей переменной x_i. Этот фактор трактуется как некоторая специфика, которая не может быть выражена через общие факторы.

Общие факторы представляют собой расчетные переменные, т.е. некоторые новые характеристики изучаемой системы.

Уравнения (4), связывающие наблюдаемые величины и характеристики, позволяют построить общую модель системы. В общем случае в правых частях уравнений моделей ни коэффициенты, ни факторы не являются известными.

Допускается также линейность модели [Айвазян, 1989], т.е.

Уравнение (5) описывает основную модель факторного анализа.

Коэффициенты a_ij в выражении (5), называемые факторными нагрузками, характеризуют значимость каждого из факторов для описания i-го признака.

Рассмотрим матрицу данных. Число строк (наблюдений) в ней равно N, а число столбцов (параметров, характеристик системы) — n. Будем считать, что параметры приведены к стандартной форме, такой что

(6)

где x_ji — значение i-го параметра для j-го наблюдения,

— среднее арифметическое значение i-го параметра,

s_i — среднеквадратичное отклонение i-го параметра (s_i² — дисперсия i-го параметра).

Стандартная форма определяет возможность сопоставления измеряемых количественных характеристик и устраняет влияние размерности, вводя единый для всех показателей масштаб.

Матрицу данных с такими параметрами обозначим X. Ее i-й столбец отображает j-ю характеристику исследуемой системы. Введем в рассмотрение N-мерное пространство наблюдений. В этом пространстве i-й столбец матрицы данных определяет некоторую точку. Вектор значений на объектах наблюдений общего p-го фактора Z_p и аналогичный вектор характерного i-й характеристики также можно рассматривать как точки введенного N-мерного пространства.

Множество векторов {Zp, p=1..m} образуют матрицу Z размером N1 m, а множество векторов {Ui, i=1..n} — матрицу U размером N1 n. Через А обозначим матрицу факторных нагрузок (ее размер n1 m), а через D — матрицу остатков (нагрузок характерных факторов). Более подробное описание факторной модели в матричном виде приведено в [Жуковская, 1976].

Используя введенные матрицы, уравнения (5) можно переписать в следующем виде:

.

(7)

Главной задачей факторного анализа является определение элементов матрицы A факторных нагрузок. При этом считается неизвестным число m общих факторов. Матрица А характеризует степень связи между каждыми из n рассматриваемых параметров и m факторами, выявленными в пространстве условий. В соответствии с поставленной задачей необходимо, чтобы число m было много меньше n, а уровень потерь информации достаточно мал.

Факторная матрица позволяет выделить для каждого фактора группу параметров — характеристик системы, наиболее тесно с ним связанную. Для этих целей можно использовать, например, методы целенаправленного проектирования или автоматической классификации. Тем самым открывается возможность сопоставить факторы друг с другом, дать интерпретацию факторов.

Основой для построения матрицы A служит матрица парных корреляций R размерностью n1 n, отражающая степень взаимосвязи между каждой парой параметров системы.

Существует несколько различных методов факторного анализа. Среди них можно выделить следующие:

1. Метод главных факторов.
2. Центроидный метод.
3. Метод главных компонент.

Особенности методов описаны в [Жуковская, 1976], а теоретические предпосылки и математические модели соответственно в [Айвазян, 1989].

Общим для этих методов является определение неизвестного заранее числа факторов через заранее найденные характеристики. Предполагается, что любая пара факторов (как общих, так и характерных) является ортогональной.

Для проведения анализа можно использовать метод главных компонент, как наиболее простой для реализации и наименее ресурсоёмкий из всех вышеупомянутых методов.

В методе главных компонент используется частная модель факторного анализа:

Отличие этой модели от модели (5) состоит в том, что здесь число факторов объявляется равным числу исходных параметров. Поэтому нет никаких характерных факторов, и (8) можно рассматривать как систему преобразования одних характеристик в другие.

Сущность линейного преобразования, приводящего к главным компонентам, состоит в том, что для описания состояния системы необязательно использовать какие-то исходные, непосредственно замеренные на нем признаки. Вместо этого возможен анализ существенно меньшего числа обобщающих параметров, отражающих изменения некоторых групп исходных признаков.

В [Айвазян, 1989] описывается следующая математическая модель метода главных компонент. Пусть состояние анализируемой системы описано некоторой p-мерной случайной величиной Х с вектором средних значений и ковариационной матрицей , вообще говоря, неизвестными. Определим меру информативности I_p'(Z) вспомогательной p'-мерной системы показателей в виде (3), а класс допустимых преобразований — как набор некоторых ортогональных преобразований и линейных комбинаций. Тогда при любом фиксированном p' = 1, 2, ..., p вектор исходных вспомогательных переменных определяется как такая линейная комбинация:

,

(9)

где матрица 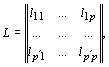а ее строки удовлетворяют условию ортогональности

(10)

Полученные таким образом переменные называют главными компонентами.

Можно сформулировать следующее определение главных компонент. Первой главной компонентой исследуемой системы показателей называется такая нормированно-центрированная линейная комбинация этих показателей, которая среди всех прочих нормированно-центрированных линейных комбинаций переменных обладает наибольшей дисперсией.

k-й главной компонентой (k= 2, 3, ..., p) исследуемой системы показателей называется такая нормированно-центрированная линейная комбинация этих показателей, которая не коррелированна с (k-1)-ми предыдущими главными компонентами и среди всех прочих нормированно-центрированных и не коррелирующих с (k-1)-ми предыдущими главными компонентами линейных комбинаций переменных обладает наибольшей дисперсией.

Исходные показатели должны быть центрированы, т.е. математическое ожидание величины x(i) должно быть равно 0.

Из определения первой главной компоненты следует, что для ее вычисления необходимо решить оптимизационную задачу вида

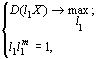(11)

где l₁ — первая строка матрицы L,

D — знак вычисления дисперсии.

Так как математическое ожидание многомерной случайной величины Х равно 0 (ЕХ = 0) и , имеем

(12)

Следовательно, оптимизационная задача может быть представлена в виде:

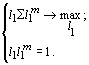(13)

Вводя функцию Лагранжа и дифференцируя ее по компонентам вектор-столбца , получаем

(14)

что дает систему уравнений для определения l₁:

,

(15)

здесь — р-мерный вектор-столбец из нулей.

Для того чтобы существовало ненулевое этой решение системы, матрица должна быть невырожденной, т.е.

.

(16)

Этого добиваются за счет подбора соответствующего значения . Уравнение (16) (относительно ) является характеристическим для матрицы . При симметричности и неотрицательной определенности матрицы (каковой она и является как ковариационная матрица) это уравнение имеет р вещественных неотрицательных корней _{1 2} ... _h 0, называемых характеристическими (или собственными) значениями матрицы .

Учитывая, что и , что следует из (14), умножением слева на l_1, с учетом , получаем

.

(17)

Поэтому для обеспечения максимальной величины дисперсии переменной z⁽¹⁾ нужно выбрать из p собственных значений матрицы наибольшее, т.е.

.

(17')

Подставляя ₁ в систему уравнений (16) и решая ее относительно l₁₁,...,l_1p, определяем компоненты вектора l₁.

Таким образом, первая главная компонента получается как линейная комбинация

где l₁ — собственный вектор матрицы , соответствующий наибольшему собственному числу этой матрицы.

Аналогично

где l_k — собственный вектор матрицы , соответствующий k-му по величине собственному значению _k этой матрицы.

Соотношения для определения всех p главных компонент вектора X могут быть представлены в виде:

где а матрица L состоит из строк l_j=(l_j1,..., l_jp), j = 1..p, являющихся собственными векторами матрицы , соответствующими собственным числам _j. При этом сама матрица L по построению является ортогональной, т.е.

Можно показать, что критерий информативности метода главных компонент может быть представлен в виде

,

(22)

где ₁, ₂, ..., _p — собственные числа ковариационной матрицы вектора X, расположенные в порядке убывания.

Такое представление критерия информативности дает некоторую основу при внесении решения о том, сколько последних главных компонент можно без особого ущерба изъять из рассмотрения, тем самым сократив размерность исследуемой системы признаков.

Анализируя с помощью (22) изменение относительной доли дисперсии, вносимой первыми p' главными компонентами, и сравнивая ее с некоторым пороговым значением, можно разумно определить число компонент, которое целесообразно оставить в рассмотрении.

В качестве примера рассмотрим функционирование банковской системы обслуживания пластиковых карточек (БСОПК). Исходными данными для решаемой задачи служат ряды динамики (временные ряды), которые получаются путем регистрации данных — показателей работы БСОПК через определенные промежутки времени. В качестве примера будем рассматривать следующие показатели:

1. Остатки на карт-счетах банка (п1) — один из основных источников получения прибыли Центра обслуживания пластиковых карточек.
2. Количество VIP-клиентов (п2).
3. Число обычных клиентов (п3).
4. Число банкоматов (п4) — характеризует развитие сети банкоматов и банковской системы коммуникаций.
5. Число филиалов (п5) — характеризует развитие “географической” структуры банка и число пунктов выдачи наличных.
6. Число POS-терминалов (п6) — характеризует степень развития банковской сети приема и обслуживания пластиковых карт.
7. Количество операций по выдаче наличных денег, происходящих в сети обслуживания банковского центра (п7). Инициаторами операций являются клиенты банка.
8. Количество операций покупки, происходящих в сети приема пластиковых карточек БСОПК (п8). Инициаторами операций являются клиенты банка.
9. Количество операций по выдаче наличных денег, происходящих в сети приема пластиковых карточек БСОПК (п9). Инициаторами операций являются клиенты других банков, имеющие пластиковые карточки.
10. Количество операций покупки, происходящих в сети приема пластиковых карточек БСОПК (п10). Инициаторами операций являются клиенты других банков, имеющие пластиковые карточки.
11. Число отказов каналов связи банковской сети приема пластиковых карточек (п11).
12. Число отказов каналов и оборудования связи с международной платежной системой (п12).
13. Число отказов аппаратно-программного комплекса процессингового центра (п13).
14. Число сотрудников (п14).
15. Число “зарплатных” предприятий, обслуживаемых банком (п15).

Выбранные параметры не претендуют на полноту описания, однако характеризуют работу банковского центра с разных сторон. Среди них можно выделить несколько групп характеристик. Так, параметр 1 можно отнести к финансовым показателям работы; 2, 3, 15 — характеризуют развитие клиентской базы и активность работы отдела развития; 4–6 — развитие сети обслуживания; параметры 7–10 описывают загруженность процессингового центра; 11–13 характеризуют надежность работы процессингового центра; 14 — характеризует развитие организационной структуры центра.

Схему решения поставленной задачи с использованием метода главных компонент можно представить в виде последовательного преобразования следующих матриц: исходных данных, парных корреляций, факторных нагрузок, расстояний между параметрами по отдельным факторам.

Подготовительным этапом вычисления является определение парных коэффициентов корреляции исходных временных рядов. Для вычисления этих коэффициентов необходимо отсутствие в рядах динамики трендов и автокорреляций. Описание соответствующих методов можно найти в [Ефимова, 1996].

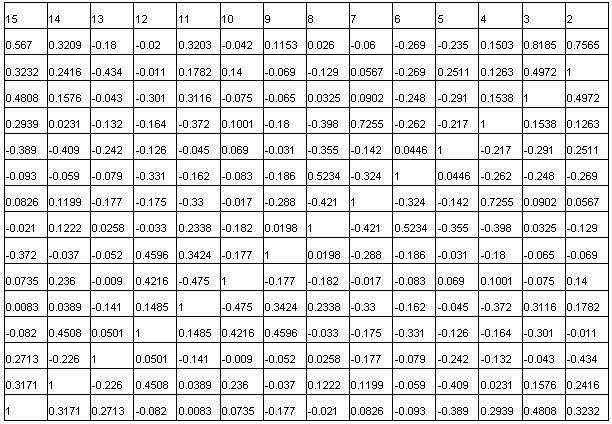
Следующим шагом обработки данных является расчет корреляционной матрицы К, состоящей из соответствующих коэффициентов линейной парной корреляции. Коэффициент рассчитывается по следующей формуле:

,

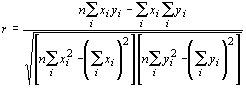(23)

здесь n — число уровней в ряду динамики;

x_i — i-й уровень ряда X;

y_i — i-й уровень ряда Y.

Матрица корреляций приведена в приложении.

В [Уилкинсон, 1997] описаны различные алгоритмы нахождения собственных чисел и векторов для симметричных матриц (матрица корреляций — симметричная, неотрицательно определенная матрица). Выбор конкретного алгоритма зависит от размера и структуры матрицы К.

Метод Якоби. Этот метод — наиболее изящный из всех представленных. Сама процедура очень компактна и легко реализуема, повышенное внимание уделяется точности получаемого решения. В данном методе используется тот факт, что существует итерационная процедура, которая приводит исходную симметричную матрицу к диагональному виду с помощью последовательности элементарных диагональных преобразований (так называемых вращений Якоби, или плоских вращений). Процедура построена таким образом, что на (k+1)-м шаге осуществляется преобразование вида

(24)

где U_k = U_k (p,q,0 ) — ортогональная матрица, отличающаяся от единичной только элементами u_pp = u_qq = cos0 и u_pq = -u_qp = sin0 . Предлагается выбирать в матрице A_k максимальный по модулю наддиагональный элемент a_pq и затем осуществлять плоское вращение на такой угол 0 , чтобы в матрице A_k+1 элемент a_pq стал равным 0. Главным недостатком метода Якоби является большое время для вычислений и высокая ресурсоемкость [Уилкинсон, 1y97], однако простота его реализации, надежность и хорошая сходимость делают его достаточно привлекательным для обработки матриц небольшой размерности. При исследовании сложных систем, имеющих большое количество определяющих характеристик, рекомендуется использовать другие методы нахождения собственных чисел и векторов.

В табл. 2 представлены результаты вычисления собственных чисел методом Якоби для исходной корреляционной матрицы. Значения собственных чисел отсортированы в порядке убывания.

Следует отметить, что значения собственных чисел больше 0. Это является результатом симметричности и неотрицательной определенности корреляционной матрицы.

Каждое собственное число характеризует конкретный найденный фактор исследуемой модели. Вес фактора в общей совокупности из М главных компонент (М в исследуемой системе равно 15) определяется по формуле:

.

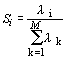(25)

Необходимо отобрать некоторое число найденных главных компонент, наилучшим образом описывающих систему. Анализируя с помощью (27) изменение относительной суммарной доли дисперсии, вносимой i-ми наибольшими по весу главными компонентами — факторами, в зависимости от числа этих компонент, можно определить необходимое число факторов, которое нужно оставить в рассмотрении. Проанализируем зависимость критерия информативности представленного в виде (22), от числа входящих в его числитель собственных чисел:

.

(26)

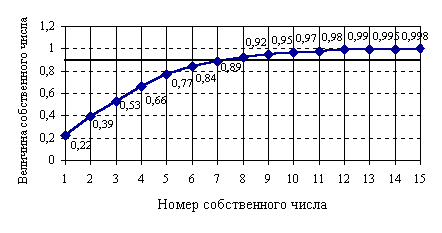
График такой зависимости представлен на рис. 1. Для определения необходимого числа факторов зададим некоторую пороговую величину критерия I_пор. Эта величина определяет точность модели. В исследуемой системе I_пор=0,75. Анализируя график, можно сказать что для дальнейшего рассмотрения достаточно оставить пять первых факторов.

Рис. 1. Зависимость критерия информативности от числа входящихв его числитель собственных чисел

Собственные векторы, соответствующие отобранным факторам, образуют матрицу факторных нагрузок (табл. 3). Анализ этой матрицы позволяет провести группировку показателей исследуемой системы.

№ параметра	Фактор
	1	2	3	4	5
	= 3,27	= 2,60	= 2,03	= 1,96	= 1,59
1	0,478	-0,252	0,030	0,053	0,040
2	0,446	-0,095	0,166	-0,243	0,018
3	0,420	-0,176	0,083	0,264	-0,007
4	0,256	0,420	-0,040	0,094	-0,105
5	0,108	0,096	0,425	-0,446	-0,024
6	-0,248	-0,068	0,420	0,024	0,374
7	0,193	0,448	-0,050	0,081	-0,184
8	-0,147	-0,350	0,206	0,092	0,326
9	-0,058	-0,297	-0,269	-0,182	-0,348
10	0,057	0,199	-0,230	-0,315	0,450
11	0,080	-0,473	0,002	0,023	-0,319
12	-0,032	-0,143	-0,522	-0,391	0,097
12	-0,167	-0,008	-0,311	0,466	0,145
14	0,215	-0,096	-0,231	-0,181	0,387
15	0,332	-0,038	-0,111	0,331	0,317

Определим меры сходства (близости) между исследуемыми объектами. Основным свойством вычисленных компонент является ортогональность собственных векторов.
Пусть число отобранных векторов есть m (m < M). Тогда множество собственных векторов можно рассматривать как m-мерную ортогональную систему координат, а множество параметров — как некоторую группу точек в этом пространстве. Тогда факторная нагрузка i-го параметра системы на j-ю главную компоненту-фактор есть проекция i-й точки на j-ю координатную ось. Таким образом, в качестве меры сходства параметров исследуемой системы можно рассматривать расстояние между точками в пространстве факторов, вычисляемое по формуле

.

(27)

Задача группировки совокупности свойств состоит в требовании разбиения всей совокупности из пятнадцати свойств на некоторое число однородных классов. При этом исходная информация может быть представлена в виде матрицы попарных расстояний между параметрами-точками. Понятие однородности основано на предположении, что геометрическая близость двух или нескольких параметров означает близость их “физического” состояния, их сходство. Математическая постановка задачи группировки [Айвазян, 1989] требует формализации понятия качества разбиения. С этой целью введем в рассмотрение понятие критерия (функционала) качества разбиения Q(S), который задает способ сопоставления с каждым возможным разбиением S заданного множества параметров на классы, некоторого числа Q(S), оценивающего (в определенном смысле) степень оптимальности разбиения. Математическая задача поиска наилучшего разбиения S^* сводится к решению оптимизационной задаче вида

,

(28)

где А — множество всех допустимых разбиений.

На практике выбор функционала качества разбиения обычно осуществляется весьма произвольно, особую роль играют эмпирические и интуитивные соображения [Айвазян, 1989]. Точной формализованной схемы не существует.

Введем понятие кратчайшего незамкнутого пути, соединяющего все N точек исходной совокупности в связный неориентированный граф с минимальной суммарной длиной ребер. Под длиной ребра понимается расстояние между соответствующими точками совокупности. Построение такого графа можно начать с пары наиболее близких точек. Если таких пар несколько, то выбирается любая из этих пар. Пусть это будут параметры с номерами i₀ и j₀. Затем с помощью сравнения расстояний d(X_i0,X_j) {j = 1, 2, ..., m;
j=i₀; j= j₀} и d(X_j0,X_q) {q = 1, 2, ..., N; q= i₀;q= j₀} определяются точки X_m(i0) и X_m(j0) , наименее удаленные соответственно от X_i0 и X_j0, и выбирается ближайшая из них X_m0, т.е. X_m0 = X_m(i0), если d(X_i0,X_m(io))< d(X_j0,X_m(jo)), и X_m0=X_m(j0) соответственно, если d(X_j0,X_m(jo))<d(X_i0,X_m(io)). Затем точка X_m0 пристраивается к X_i0 или X_j0 в зависимости от того, к какой точке она ближе. Далее сравниваются расстояния d(X_i0,X_j), d(X_j0,X_q) и d(X_m0,X_v) {j= i₀, j₀, m₀; q= i₀, j₀, m₀; v =i₀,;j₀,m₀} и т. д. Полученный граф представлен на рис. 2 (ребра графа пронумерованы в порядке убывания длины ребра).

Рис. 2. Классификационный граф

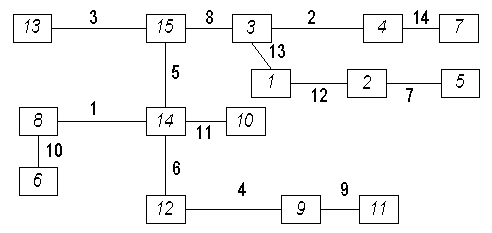
Пусть Ч _i(l) — i-е ребро части графа, отнесенной к l-му классу — группе. Всего таких ребер будет n_l - 1, пусть — минимальное из ребер, непосредственно примыкающих к ребру, и относится к l-му классу, если таковое имеется. Пронумеруем в определенном порядке граничные (“разрубленные”) ребра ₁, ₂ ,..., _k-1 таким образом, чтобы имелось взаимно однозначное соответствие между номерами граничных ребер и примыкающих к ним классов, за исключением одного, геометрически представленного одним из хвостов графа. Выбрасывая ребра ₁, ₂ ,..., _k-1, получаем k связанных графов, что соответствует разбиению всей совокупности признаков на k групп.

Выделим, согласно [Айвазян, 1989], некоторые величины u_i, характеризующие как межгрупповую, так и внутригрупповую структуру наблюдений при фиксированном разбиении на классы, чтобы существовала некоторая функция Q(u₁, u₂,...) от этих величин, которую мы могли бы считать характеристикой качества разбиения. Величины[Елкина, 1987] u_i определены следующим образом:

,

где 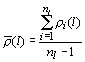— средняя длина ребер l-го класса. Величина u₁ характеризует степень близости элементов внутри классов;

— степень удаленности классов друг от друга;

— степень равномерности распределения общего числа классифицируемых наблюдений по классам.

Эмпирический перебор различных вариантов общего вида функционала качества разбиения привел авторов [Елкина, 1987] к следующей формуле:

.

(29)

Лучшим разбиениям соответствуют большие численные значения функционала Q, так что в данном случае следует найти такое разбиение S^*, при котором:

.

(30)

Зависимость критерия качества разбиения от количества “разрубленных” ребер, имеющих максимальную длину, приведена на рис. 3.

Рис. 3. Зависимость критерия качества разбиения от количества “разрубленных” ребер графа

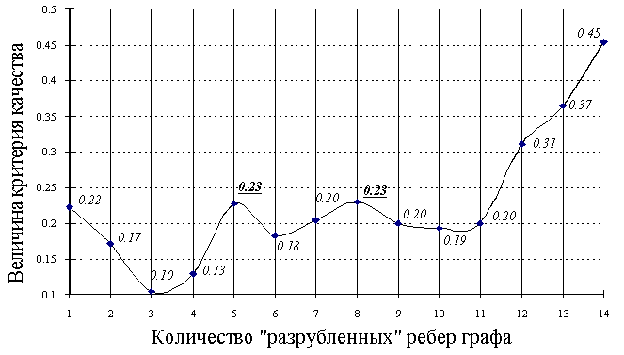
Удаление ребер графа происходит в порядке уменьшения их длины.

Максимум критерия достигается при четырнадцати “разрубленных” ребрах, что соответствует разбиению всей совокупности признаков на пятнадцать классов. Однако такое разбиение не соответствует целям поставленной задачи — выделению групп взаимосвязанных признаков.

В этой связи следует выделить два локальных максимума функции критерия: в точках, соответствующих разбиению на шесть и девять групп. Вариант разбиения на шесть классов более предпочтителен, поскольку является более оптимальным с точки зрения одной из целей общей задачи — снижения размерности исходной совокупности данных.

В результате обработки исходных данных были получены следующие группы характеристик БСОПК:

Группа 1

Группа 2

Группа 3

Группа 4

Группа 5

Группа 6

Заключительной стадией анализа является интерпретация полученных результатов. Эта стадия должна проводится экспертом БСОПК. Ниже приводится небольшой пример подобного анализа.

Группа 1. Эта группа объединяет в себе показатели, описывающие состояние клиентской базы (параметры (п2) и (п3)), и показатель, определяющий прибыль банка, получаемую от использования его клиентами пластиковых карточек. Можно утверждать, что прибыль банка сильно зависит от количества клиентов и соответственно для ее увеличения необходимо увеличение клиентской базы. Количество клиентов, в свою очередь, зависит от деятельности филиалов, играющих важную роль в формировании клиентской базы всего банка, — их количества (п5) и от количества договоров на выплату заработной платы с различными предприятиями (п15).

Группа 2. Связь между параметрами (п10) и (п12) объясняется тем, что интенсивность потока транзакций, уходящих в международную пластиковую систему (МПС), определяется в основном количеством операций покупки, совершаемых клиентами других банков (а не операциями выдачи наличных), так как правилами МПС запрещается удержание процентов с суммы операции. Клиент оплачивает только стоимость оказанных услуг.

На качество обслуживания в этом случае влияет надежность коммуникаций между банком и МПС, зависящая от потоков операций покупки.

Включение в эту группу параметра (п14) не является очевидным.

Группы 3 и 4. Анализ этих групп показывает, что в рассматриваемый промежуток времени рост активности клиентов банка (увеличение количества операций) сдерживается небольшими размерами банковской сети приема и обслуживания пластиковых карточек.

Группа 5. Группа 5 является самой “спорной” из всех перечисленных. Объем операций выдачи наличных составляет лишь небольшой процент от общего количества операций, совершаемых в банковской сети приема пластиковых карточек и, следовательно, не может определять количество сбоев в этой сети. Использование этой группы в дальнейшем не является целесообразным.

Группа 6. Наличие в группе 6 одного показателя числа отказов аппаратно-программного комплекса (АПК) процессингового центра (п13) свидетельствует о том, что ни один из рассматриваемых признаков в анализируемый период времени не оказывает существенного влияния и не определяется этим параметром.

При проведении анализа необходимо отметить решающую роль эксперта при контроле и вынесении решения о достоверности полученных результатов. Разработанный алгоритм не является универсальным заменителем умственной деятельности эксперта, а служит инструментом, автоматизирующим вычислительную часть статистического анализа показателей, характеризующих состояние и изменения предметной области.

1. Программная реализация разработанного алгоритма обработки статистических данных может быть использована как самостоятельный модуль предварительной обработки данных в составе экспертных систем поддержки принятия решений в области обслуживания банковских пластиковых карточек и анализа деятельности БСОПК. Не существует принципиального ограничения для использования данного алгоритма при анализе других предметных областей.
2. Для контроля полученных результатов необходимо использование экспертных оценок и знаний сотрудников БСОПК. Программные реализации могут быть использованы как средства автоматизации (но не полной замены) исследовательской деятельности при выявлении соподчиненных целей и задач.
3. Для проведения дальнейших исследований необходимо шкалирование исследуемых показателей.
4. Для организации взаимодействия с пользователем рекомендуется алгоритм, представленный на рис. 4.

Реализация подобного алгоритма требует разработки специальных элементов пользовательского интерфейса.

Рис. 4. Организация взаимодействия с пользователем