1. ПОСТАНОВКА ЗАДАЧ ИССЛЕДОВАНИЯ

Исследование проводилось в два этапа, получивших следующие условные названия: 1-й этап — "Разработка ассоциативного словаря"; 2-й этап — "Разработка ассоциативного тезауруса".

На первом этапе осуществлялся ассоциативный эксперимент и первичная обработка полученных данных. Основными результатами работ этого этапа являются: разработанный программный комплекс поддержки процедур и операций эксперимента, анкеты проведенного опроса, заполненная база данных эксперимента и полученные на основе ее обработки материалы Ассоциативного словаря информационных технологий (АСИТ).

Задачи первого этапа: определение списка слов-стимулов, генерация анкет, подготовка их к печати и печать, создание базы данных исследования, проведение анкетирования, ввод и формальный контроль данных анкетного опроса, заполнение базы данных исследования, статистический анализ базы данных, формирование статей ассоциативного словаря, подготовка ассоциативного словаря к печати.

На втором этапе был разработан и апробирован инструментарий для проведения кластерного анализа результатов ассоциативного эксперимента, построена базовая (феноменологическая) модель связей "стимул — стимул" Ассоциативного тезауруса информационных технологий (АТИТ).

Задачи второго этапа: обзор методов кластерного анализа, разработка интерфейса базы данных исследования и программного модуля построения тезауруса, разработка меры оценки силы связи между словами-стимулами и инструментария ее оценки, подготовка данных к кластерному анализу (корректировка нулевых значений меры связи, преобразование значений силы связи в расстояния), кластерный анализ множества слов-стимулов на основе матрицы расстояний.

Рассмотрим более подробно постановку некоторых задач исследования.

1.1. Разработка ассоциативного словаря

Генерация анкет

При проведении анкетирования важным является получение на каждое из слов-стимулов одинакового количества слов-реакций. Кроме этого нужно стремиться к исключению внешних организационных факторов, влияющих на ответы респондента.

Два основных фактора оказывают влияние на количество ответов (слов-реакций) опрашиваемых: во-первых, неравномерность представления слов-стимулов в анкетах — в некоторых анкетах какие-то слова-стимулы могут повторяться или отсутствовать; во-вторых, отсутствие слов-реакций на некоторые слова-стимулы — по условию эксперимента респонденты в своей анкете могут не указать слово-реакцию на какое-то слово-стимул.

В числе внешних факторов отметим: а) факторы формы анкеты, влияющие на удобство работы с ней респондентов — геометрические размеры, формат и шрифт текста и др.; б) факторы содержания анкеты — количество слов-стимулов и порядок их расположения, особые сочетания слов-стимулов.

Некоторые сочетания слов-стимулов могут определять ответы опрашиваемых или оказывать влияние на них. Например, при имеющейся в анкете последовательности

стимул1... реакция1

стимул2... реакция2

можно обнаружить, что реакция2 является реакцией не на слово стимул2, а на совокупность слов (стимул1, реакция1, стимул2) целиком, так как предыдущая строка и, следовательно, предыдущая мысль остались в памяти испытуемого.

Замечено, что при ручном способе составления анкет, когда сам исследователь выбирает слова-стимулы, неравномерное распределение их по анкетам и появление особых и повторяющихся сочетаний весьма частое явление. При таком способе из-за значительной трудоемкости нереальными являются какие-либо замены в уже сформированных анкетах слов-стимулов, а также поиск и устранение их особых или часто встречающихся сочетаний.

Забота о качестве результатов эксперимента заставляет исследователя стремиться к тому, чтобы, во-первых, конкретные сочетания слов-стимулов встречались с наименьшей вероятностью, а во-вторых, они были бы наиболее разнообразными, так чтобы их влияние было неоднозначным. Такого результата можно добиться при использовании формальных (статистических) методик генерации анкет, основанных на методах случайной выборки слов-стимулов из их общего списка. Сформулируем задачу генерации анкет исследования в следующем виде:

Необходимо из общего списка слов-стимулов, расположенных в случайном порядке, сгенерировать множество подсписков, для которого разброс частот появления каждого слова-стимула в этом множестве был меньше некоторой первоначально заданной величины.

Формальное описание.

Обозначим:

N — общее количество стимулов;

n — количество анкет;

m — количество слов-стимулов, представленных в анкете.

Пусть А — массив анкет.

где для

Суть задачи генерации анкет заключается в выполнении следующих двух требований:

1. Запрещается повтор любого стимула w_ij в одной анкете i, т.е.:

2. Максимальный разброс частоты f_k проявления стимула k ограничен: он должен быть как можно ниже. Идеальным считается случай, когда частоты имеют либо наперед заданное значение F, либо значение F+1, т.е.

Подготовка анкет к печати

Анкета должна содержать следующие поля: номер анкеты; возраст, пол, специальность и родной язык респондента; дату, время начала и конца заполнения анкеты; список стимулов; титул.

В анкете в списке стимулов слева от каждого слова-стимула должен присутствовать его код, справа — свободное место, куда респондент записывает свое слово-реакцию. Код стимула используется в технологии клавиатурного ввода данных, в ней набирается не само слово-стимул, а его код.

Титул анкеты должен представлять собой один из следующих текстов: "Ассоциативный эксперимент — май-июнь 1999 г. — руководитель: к.т.н., доц.Филиппович Ю.Н." — для опроса русскоязычных респондентов; "Expérience linguistique associative —sept.1999 — MGTU/ECL — Dr. Pr. Iouri N. Philippovitch / Denis Dhelft" — для опроса франкоязычных респондентов.

Анкета должна иметь вид бумажного документа формата А4, примеры представлены на рис. 1.

Формальное описание.

Пусть i Î {1..n} и A_i Î A. Респонденту выдаются следующие данные (они уже присутствуют в бланке анкеты): номер анкеты; множество пар, состоящих из кода стимула и самого слова-стимула — (w_ij,s_wij).

В результате заполнения анкеты получаются значения следующих полей: возраст (v); пол (p); специальность (q); родной язык (y); дата (d); время начала (t₀); время конца (t₁); множество реакций (r_j)_j, где r_j является словом-реакцией на слово-стимул s_j. То есть для

Создание базы данных эксперимента

База данных эксперимента предназначена для эффективного хранения информации в виде, удобном для ее последующей обработки. При этом должны быть обеспечены минимальные затраты памяти на хранение данных и время выполнения операций над ними.

Для удовлетворения этих требований традиционным является использование специальных пакетов программ — систем управления базами данных (СУБД). В исследовании использовалась реляционная СУБД Microsoft Access 97. Выбор данной СУБД был обоснован ее функциональными возможностями и распространенностью в среде возможных пользователей результатов исследования, а также знаниями и навыками исследовательского коллектива.

В случае использования реляционных моделей и соответствующих СУБД данные в таблицах должны находиться в 3-й нормальной форме. Это означает, что при разработке баз данных эксперимента должны быть выполнены процедуры нормализации структур, которые приводят к получению рациональной модели хранимых данных.

Ввод анкетных данных

Для ввода сведений, содержащихся в бумажных анкетах, полученных после проведения опроса, должны быть предусмотрены две технологии:

1) технология непосредственного ввода содержания анкет в базу данных исследования, в которой используются инструменты ввода данных, предоставленные выбранной для ее реализации СУБД;

2) независимая от конкретной СУБД технология ввода содержания анкет в текстовые файлы определенного формата и последующее импортирование их в базу данных.

Проверка введенных данных

Ошибки ввода данных могут появляться в любом поле анкеты. Все возможные ошибки следует разделить на два типа: неформальные (а) и формально-логические (б).

К ошибкам типа (а) относятся в основном ошибки ввода слов-реакций, которые представляют собой рукописные записи респондентов, сделанные порой неразборчивым почерком. Их можно обнаружить только путем чтения текстового файла введенных анкет либо по его распечатке, либо непосредственно с экрана дисплея, и сравнения с бумажной анкетой. Такие ошибки могут быть исправлены только путем клавиатурного набора.

Ошибки типа (б) могут быть обнаружены и в некоторых случаях автоматически исправлены путем формально-логического контроля вводимых данных. Ниже представлены поля, в которых можно обнаружить ошибки путем формально-логического контроля:

— значение поля возраст должно быть в некоторых пределах, в зависимости от выборки испытуемых;

— поле пол должно принимать значение или "м", или "ж";

— значения полей время и дата должны быть отформатированы;

— значение поля код каждого стимула не может быть ни нулевым, ни превышать общее количество стимулов, а также невозможно присутствие любого кода больше одного раза в одной анкете. К тому же список стимулов, представленных на каждой анкете, заранее известен. Можно сравнить список введенных кодов со списком кодов, которые должны присутствовать, и указать на расхождения.

Формальное описание.

Допустим, что проверяется анкета № i, i Î {1..n}.

A_i: (i, (w_ij,s_wij,r_wij)_{jÎ {1..m}},v_i,p_i,q_i,y_i,d_i,t_0i,t_1i).

Можно, например, проверить истинность следующих предикатов:

v_i Î {5..120}; p_i Î {"ж", "м"}; t_0i < t_1i.

Составление статей ассоциативного словаря

В базе данных эксперимента после ввода имеется множество ассоциативных пар (стимул—реакция), распределенных по анкетам. Статья ассоциативного словаря представляет собой запись слова-стимула (S) и соответствующего ему множества слов-реакций (R) — ассоциативную дефиницию, при этом для каждой из реакций указана абсолютная частота ее встречаемости в паре с данным стимулом. Для составления статей ассоциативного словаря нужно отсортировать множество ассоциативных пар по стимулу и для каждого стимула подсчитать частоту встречаемости соответствующих ему реакций.

Формальное описание.

Необходимо получить (Δ_р=1.. Δ_р=N) — ассоциативные дефиниции стимулов (s₁..s_N). Структура ассоциативной дефиниции следующая:

Δ_р = ((R_p1,f_p1)..(R_pd,f_pd)),

где R_pu — u-я реакция ассоциативной дефиниции стимула s_p; f_pu — количество ответов R_pu на стимул S_p; d = d_p — "длина" ассоциативной дефиниции Δр.

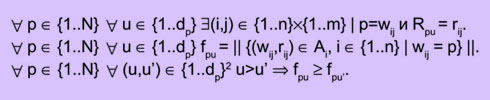
Подготовка ассоциативного словаря к печати

Средой разработки АСИТ является СУБД Access. Однако в этой среде нельзя сформировать оригинал-макет печатного издания словаря, удовлетворяющий требованиям полиграфии. Кроме этого использование функциональных возможностей СУБД Access по созданию отчетных печатных форм требует значительной дополнительной ручной работы из-за того, что автоматически списки слов в формах Access представляются в основном в виде столбцов, а для удобства чтения и экономии места на страницах печатного ассоциативного словаря лучше разместить слова по строкам, используя традиционные разделители (точки, запятые и др.). Общая трудоемкость форматирования словарных статей и страниц в СУБД Access велика, ведь количество представленных слов огромно. Технология формирования страниц печатного АСИТ включает создание запроса на экспорт словарных статей в Microsoft Word и последующую автоматическую замену специальных символов (разделителей строк) на традиционные текстовые разделители (точку с запятой и др.).

1.2. Разработка ассоциативного тезауруса

Обзор методов и алгоритмов кластерного анализа

Существует множество методов и алгоритмов кластерного анализа. Основная проблема выбора конкретного метода и какого-либо алгоритма его реализации заключается в том, что весьма трудно описать кластеры, которые ожидается получить в результате работы соответствующих программ.

Методы кластерного анализа.

Все методы можно условно разделить на три типа:

1) эвристический: задается точное определение требуемого "образа" кластеров (например, однородные точки должны находиться внутри гиперсферы радиуса R и некоего "центра тяжести"). К недостаткам этого подхода относится то, что определение типичного образа однородных групп может оказаться слишком строгим, т. е. принципиально допустимые кластеры, вид которых не соответствует критерию, отклоняются;

2) оптимизационный: требуемое разбиение соответствует минимуму заданного функционала качества. Этот подход интересен тем, что он дает чисто математическую постановку задачи классификации. Но тогда проблема заключается в выборе и выражении функционала, что чаще всего оказывается нетривиальным (не говоря о самом процессе нахождения экстремума);

3) аппроксимационный: отыскивается такое преобразование (представление) множества данных, которое раскрывает его структуру как состоящую из отдельных областей.

Эти три типа кластеризации связаны тем, что они все носят оптимизационный характер, ведь можно сформулировать первый и третий подходы (а в общем, любой подход: речь идет о математическом формализме) в виде минимизации некоего функционала. Одни методы первого типа рассматривают проблему только на уровне кластера, предполагая то, что "качественная" группировка исключительно обусловлена формированием "качественных" кластеров.

Классификация алгоритмов кластеризации

Классификация по результатам процедуры:

1) разбиение с непересекающимися классами. Результат представлен в виде кластеров: все объекты внутри найденного класса считаются тождественными, а объекты разных классов – нет;

2) разбиение с пересекающимися классами. В этом случае результаты классификации заданы:

a) либо введением степени принадлежности объекта к классу в духе теории нечетких множеств;

b) либо определением вероятности принадлежности объекта к классу;

c) либо простым перечнем объектов в зоне пересечения.

Однако такой результат может считаться неудовлетворительным для целого ряда применений, где требуется четкое разбиение множества на разные классы;

3) иерархическое дерево. Оно указывает, на какой ступени можно объединить объекты друг с другом, в зависимости от "глубины" узла объединения в дереве. На минимальной – все объекты отдельны; на максимальной – все охваченными в одном классе. Этот подход не полностью решает задачу кластеризации, поскольку после его завершения остается применить критерии, чтобы обрисовать разные классы.

Классификация по степени участия человека в процессе кластеризации:

1) человек не принимает участия в работе алгоритма: классификация производится чисто машинным способом. Тем не менее, исследователю принадлежит право отобрать меру расстояния и параметры классификации;

2) человек участвует в процессе: он принимает решения о разбиении на основании информации о классификации, которая выдана алгоритмом. При этом нужно эффективное визуальное представление данных. Одним из этих методов является метод упорядочения матрицы связи.

Классификация по заданным условиям:

1) классификация свободная: нет априорных сведений;

2) классификация с заданным числом кластеров;

3) классификация с заданным порогом внутригруппового сходства.

Измерение связей между объектами

Какой алгоритм исследователь бы ни выбрал, неотъемлемой предварительной задачей является определение меры межточечной близости (или расстояния) элементов кластеризуемого множества. Ведь любая ниже описываемая процедура принимает каким-то образом в качестве исходного данного треугольную матрицу сходств, содержащую всю информацию о связях, соединяющих объекты между собой.

Некоторые методы кластерного анализа

Метод кластеризации полным перебором.

Этот подход наиболее прост в формулировке и гарантирует достижение оптимального результата в смысле минимизации некой целевой функции.

Задается в качестве параметра желаемое число кластеров. Алгоритм пробует все разбиения, вычисляя для каждого значение целевой функции, и отбирает то, которое приводит к ее минимальному значению.

Однако по мере возрастания параметров (количества объектов и кластеров) имеет место так называемый "комбинаторный взрыв". Например, применение этого подхода для группировки 8 точек на 4 класса приводит уже к построению и расчету 1701 различных разбиений¹ (¹ См. Дюран Б. и Оделл П. Кластерный анализ. Пер. с англ. Е.А.Демиденко. Под ред. А.Я.Боярского. Предисловие А.Я.Боярского. М., “Статистика”, 1977. — 128 с. Duran B. S., Odell P. L. Cluster analysis: a survey. — Berlin, Heidelberg, New York, 1974. С. 41.). Число разбиений n объектов на m непустых подмножеств определяется числом Стирлинга второго рода и рассчитывается следующим образом:

S(n,m) = 1/m! ´ å (k=0, m, Comb(m,k) ´ (—1)^m-k ´ kⁿ).

При больших n имеем,

S(n,m) » m^n-1.

Кластеризация полным перебором — очень плохой метод с точки зрения трудоемкости. Ее применение оказывается в большинстве практических случаев нереальным.

Метод динамического программирования.

Суть этого метода заключается в целенаправленном поиске разбиения, дающего минимальное значение целевой функции. При этом сохраняется принцип к ластеризации полным перебором, но он улучшается с технической точки зрения. Основой совершенствования техники перебора являются различные идеи сокращения объема вычислений путем их направленной реорганизации.

Дженсен ² (² Там же, с. 57-64.) предлагает следующую формулировку этого подхода (формулировку "динамического программирования"):

W₀ = 0

где W — внутригрупповая сумма квадратов; M — число непустых непересекающихся кластеров; m₀ — принимает значение m₀ =m, если n і m и m0 = n ≥ m, если n < 2m; k — индекс шага; z — переменная состояния, характеризующая текущее положение процесса кластеризации на шаге k; y — то же самое, как z, но на предыдущем шаге k—1; (z—y) — множество объектов, зафиксированных в одном классе при текущем шаге (k-й созданный кластер); T(z—y) — стоимость кластера (z—y).

Дендограммы

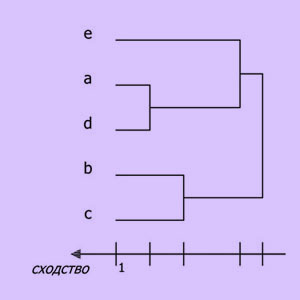
Дендограммы (или диаграммы-дерева) представляют собой графическое изображение процесса кластеризации³ (³ Там же, с. 72-73.) как некоторой последовательной группировки объектов (кластеров) на основе значений матрицы сходства (расстояний). При построении дендограммы объекты последовательно объединяются в кластеры. Сначала считается, что каждый объект представляет собой кластер. Используя меру сходства типа кластер — кластер, определяют, надо ли объединить два рассматриваемых кластера в один или при каком ее значении это сделать.

Именно это значение отражается на дендограмме горизонтальной (или вертикальной) позицией узла. Здесь соединяются ветви дендограммы, соответствующие группирующимся классам.

Диаграммы-дерева обычно выглядят следующим образом:

Интерфейс БД исследования и модуля построения тезауруса

Программный модуль построения тезауруса должен быть реализован как СУБД — независимый комплекс программ, так как в СУБД Access отсутствуют эффективные инструменты программирования, необходимые для решения задач кластерного анализа, лежащего в основе построения ассоциативного тезауруса.

Модуль построения тезауруса должен использовать всего лишь одну таблицу, имеющую следующую структуру:

<код стимула><код реакции><частота ассоциативной пары>

Модуль должен осуществлять только вычислительные операции, поэтому ему нужна исключительно числовая информация. Для этих операций надо создать специальную структуру данных, которая, с одной стороны, отражала бы структуру самого ассоциативного словаря как такового, а с другой — позволяла бы исследователю абстрагироваться от конкретных данных ассоциативного эксперимента (слов-стимулов и слов-реакций) и сосредоточиться на разработке меры связи.

В результате работы модуля построения тезауруса должна получаться следующая таблица группировок слов-стимулов по разным кластерам:

<код кластера><код стимула>

Эта таблица затем должна импортироваться в базу данных для предварительного оформления тезауруса (замены кода стимула самим словом-стимулом).

Таким образом, требуется:

а) в базе данных каждому слову-реакции поставить в соответствие цифровой код;

б) экспортировать во внешний файл список ассоциативных пар в числовом виде, снабженных их частотой проявления;

в) в программном модуле построения тезауруса прочитать этот файл, извлечь из него информацию и заполнить поля внутренней структуры данных ассоциативного тезауруса по аналогии со структурой ассоциативного словаря;

г) построенный ассоциативный тезаурус экспортировать в базу данных через внешний текстовый файл.

Формальное описание.

В качестве формального описания этой задачи приведем условные обозначения обработанных данных:

А. В базе данных существует следующая таблица: <i><k_i><w_i>, где i Î {1..m´ n} — номер ассоциативной пары; k_i Î {1..N} — код стимула; w_i — слово-реакция.

Нужно придать каждому слову-реакции собственный код реакции k' и подсчитать f_j — число раз, когда появляется ассоциативная пара s(k_j), r(k'_j), где: j — индекс ассоциативной пары j Î {1..z}, z — количество разных ассоциативных пар; s(k_j) — слово-стимул, имеющее код k_j; r(k'_j) — слово-реакция, имеющая код k'_j.

Б. Модулю построения ассоциативного тезауруса передается файл, содержащий множество E = (k_j,k'_j,f_j), j Î {1..z}, в формате передачи прямого ассоциативного словаря.

В. Для выполнения операций построения ассоциативного тезауруса фактически нужно преобразовать прямой ассоциативный словарь из формата передачи во внутренний формат модуля, для которого создана специальная структура данных, полностью отражающая структуру ассоциативного словаря.

Пусть D — объект со структурой данных, соответствующих совокупности статей ассоциативного словаря. D = {a₁..a_N}. Имеется " i Î {1..N} ассоциативная статья a_i = (k_i,ρ_i), состоящая из кода стимула k_i и ρ_i — множества пар (реакция, частота), т.е.: " i Î {1..N}, $ d Î η (η означает здесь и в дальнейшем множество положительных целых чисел), $ (c_i1..c_id) Î η^d, $ (f_i1..f_id) Î η^d | ρ_i = ((c_i1,f_i1)..(c_id,f_id)) и (k_i, c_ij, f_ij) Î E.

Г. В результате работы модуля построения тезауруса получается распределение множества S = {k₁..k_N} кодов слов-стимулов по ρÎ η кластерам. Это распределение назовем кластеризацией C = {γ₁.. γ_p}. Если P(S) — множество подмножеств S, то свойства кластеризации следующие:

и и

Полученная кластеризация экспортируется в базу данных в виде файла следующего формата (i, γ_ij), где: i Î {1..p} — номер кластера, а γ_ij — код j-го слова-стимула кластера i.

Мера оценки силы связи между словами-стимулами

Следующее правило-идея лежит в основе фиксации ассоциативных отношений между словами-стимулами:

два стимула считаются ассоциативно связанными в том случае, если их ассоциативные дефиниции, представляющие множества слов-реакций, пересекаются (т.е. в их ассоциативных "толкованиях" имеется хотя бы одно общее слово-реакция), при этом может учитываться степень важности конкретного слова-реакции, о котором свидетельствует, в частности, его частота встречаемости.

Итак, мера оценки силы связи является функцией двух словарных статей. По правилу-идее, чем сильнее сравниваемые слова-стимулы связаны между собой, тем более схожи их ассоциативные дефиниции, тем больше число общих слов-реакций и тогда, должно быть, больше значение этой функции.

Следует заметить, что построение и настройка меры силы связи существенно влияет на содержание тезауруса. Если, например, мера слишком селективная, то она будет выдавать большие величины на те пары слов, которые очень близки по смыслу, и малые на остальные пары. Таким образом, полученный тезаурус может оказаться тривиальным из-за того, что он состоит из большого количества маленьких групп слов, в том числе и групп, насчитывающих всего лишь одно слово, что считается неудовлетворительным результатом.

Формальное описание.

Пусть μ — мера оценки силы связи.

где S = {k₁..k_N} — множества кодов стимулов, — множество вещественных чисел.

На самом деле мера работает над так называемым пересечением ассоциативных дефиниций π _ii’:

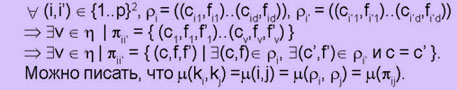
Инструментарий оценки меры связи

Разработав свою меру связи, исследователь получает множество значений μ(i,j). На этом этапе, для того чтобы проверить, связывает ли эта мера слова действительно соединенные по смыслу, ему нужно просмотреть список типа

<слово-стимул i ><слово-стимул j><значение силы связи>,

упорядоченный в порядке убывания μ. Для этого необходимо сформировать следующий документ:

<главное слово-стимул>

<связанный стимул 1, значение μ между ними)>,

<связанный стимул 2, значение μ между ними> и т.д.

Формальное описание.

S = {s₁..s_N} — слова-стимулы. Надо сформировать следующее множество:

{(s_i, {(s_j, μ(i,j)), j Î {1..N}, j ¹ i}), i Î {1..N}}.

Корректировка нулевых значений меры сил связи

Если взять произвольную пару стимулов, то возможно, что их ассоциативные дефиниции вообще не пересекаются, т.е. у них нет никакой общей реакции. Мера оценки силы связи в этом случае имеет нулевое значение. При отображении таких результатов в матрице сил связи Z может наблюдаться большое количество нулей. Из-за этого в итоге кластеризации следует ожидать результаты плохого качества, будь то большое количество маленьких тривиальных кластеров, будь то множество кластеров, содержащих слова, не имеющие смыслового отношения.

Матрицу взаимосвязанных слов, можно интерпретировать как граф или сеть. Если в матрице Z есть нули, то это означает, что сеть неполносвязанная. Иными словами, между двумя вершинами графа не всегда имеется ребро. Конечной целью кластеризации является получение нескольких подмножеств слов, т.е. разрезание сети на полносвязанные подсети.

Для осуществления кластеризации (выделения полносвязанных подсетей) воспользуемся случаем присутствия нулевых значений сил связи в матрице.

Возможно, что сеть уже состоит из двух или более подсетей. В этом случае оказывается, что, начиная с некоторого слова и переходя от слова к слову по ребрам графа, какой бы путь ни выбирали, есть особые слова, которые вообще не достигаются. Такое уже фактически существующее разбиение может быть выявлено путем анализа расположения нулевых значений матрицы Z. В результате анализа получаются подмножества слов-стимулов со следующими характеристиками: а) в любом из них два стимула являются либо непосредственно связанными ненулевой силой связи, либо связанными через некоторую цепочку стимулов, соединенных ненулевой связью; б) два стимула, взятые из разных подмножеств, никак не связаны, даже какой бы то ни было цепочкой. Итак, получилось предварительное разбиение общего множества стимулов.

Если сеть исходно является полносвязанной, то запуск модуля кластерного анализа не даст никакого результата и это будет означать, что для любой исходной пары слов-стимулов нашлась цепочка, соединяющая их. Иными словами, попытка осуществить предварительное разбиение оказалась несостоятельной из-за того, что данная сеть стимулов уже является кластером. В дальнейшем будем рассматривать (допускать) только одно такое подмножество.

Если в матрице сил связи остаются нулевые значения для тех пар слов, у которых были обнаружены цепочки связей, то модуль кластеризации отнесет соответствующие слова к разным кластерам. Но в эксперименте могут быть случаи, когда существует система (слово1, слово2, слово3) такая, что мера связи даст нулевое значение над парой (слово1, слово3), а большие значения над (слово1, слово2) и (слово2, слово3). Это значит, что есть такие пары слов, между которыми существует нулевая сила связи, но которые надо все равно соединить в один и тот же кластер, если учесть "силу" цепочки, имеющейся между ними. Учет цепочки фактически устанавливает новую связь, правда, "второй степени" по сравнению со связью, непосредственно получаемой из меры. Назовем такую новую связь "псевдосвязью". Значение псевдосвязи заменяет ноль в матрице, "уточняя" его.

Таким образом, получаем следующую формулировку задачи подготовки данных к кластерному анализу в части корректировки нулевых значений меры сил связи:

1. Используя нулевые значения матрицы сил связи, предварительно разбить исходное множество слов-стимулов на подмножества.

2. Установить псевдосвязи между словами-стимулами с нулевой связью, оценивая и присваивая им значение "силы" минимальной цепочки.

Формальное описание.

Обозначим B = {1..N}. Пусть Z = (μ_ij)_1≤i,j≤N — матрица сил связи. Назовем S = {w₁..w_N} и обозначим ≡ и ~ — отношения эквивалентности над S²:

т.е. w_i ≡ w_j Û "w_i и w_j непосредственно связаны ненулевым значением меры" и w_i ~ w_j Û "существует цепочка ненулевых сил связи, соединяющая w_i и w_j".

Итак, получить предварительное разбиение — это создать S_/~, множество классов эквивалентности отношения ~:

Пусть S_/~ = {Σ₁.. Σ_K} – классы эквивалентности.

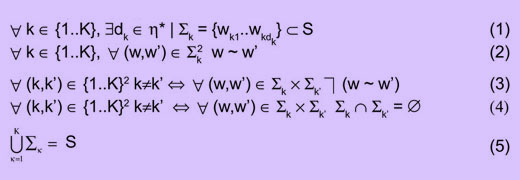
В (3) ù обозначает логическое отрицание.

Для упрощения обозначений будем считать, что S=Σ₁ (т.е. для K=1: " (i,j) Î B², w_i ~ w_j). Будем называть T_ij цепочкой ассоциативных связей между двумя стимулами i и j, тогда

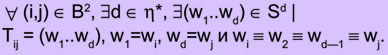
Если Q _ij является множеством цепочек между словами w_i и w_j, то

Пусть — множество всех возможных цепочек. Создадим функцию оценки цепочки:

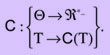
Если T = (w₁..w_d), то C может учесть значение d и все значения {m (w_i,w_i+1), i Î {1..d—1} } — значения сил связи между словами цепочки:

где t — одна из минимальных цепочек, по оценке функции оценки цепочек С.

Итак, построим функцию минимальной цепочки:

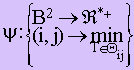
Установление псевдосвязей — это замена нулевых значений матрицы Z = (m _ij)_1≤i,j≤N значением ψ(i,j). Получается, что скорректированная матрица сил связи Z' = (λ_ij) _1≤i,j≤N не содержит ни одного нуля и строится следующим образом:

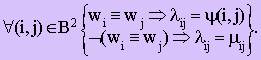
Преобразование значений силы связи в расстояния

Решение этой задачи необходимо, так как алгоритм кластеризации опирается не на значение меры близости между объектами (мера силы связи является мерой близости), а на значение меры расстояния. Следует заметить, что в результате преобразований получить расстояние в математическом смысле этого слова не удастся, ведь способ сравнения слов друг с другом не может обеспечить удовлетворение неравенства треугольника. Например, в системе μ(s₁,s₂)=a, μ(s₂,s₃)=b, μ(s₁,s₃)=0, какая бы методика преобразования меры близости в расстояние ни использовалась, расстояние |s₁s₃| всегда будет больше суммы |s₁s₂|+|s₂s₃|. Эта проблема остается даже при отсутствии нулевых связей.

Для того чтобы преобразовать значения меры силы связи в расстояние, можно воспользоваться некоторой убывающей функцией преобразования. Функция преобразования также играет нормирующую роль в процессе подготовки данных к кластерному анализу, и, являясь последним звеном в цепи подготовки данных для кластерного анализа, она не должна "портить" информацию об ассоциативных отношениях. Исследователю предстоит решение тонкой задачи настройки и согласования: меры связи, функции оценки цепочек связей и функции преобразования.

Формальное описание.

Имеется скорректированная матрица сил связи Z' = (λ_ij) _1≤i,j≤N. Необходимо получить Ω = (ω_ij) _1≤i,j≤N — матрицу расстояний.

Построим функцию преобразования:

F должна быть строго убывающей: .

Кластерный анализ множества слов-стимулов

В данной задаче слова-стимулы рассматриваются как объекты, которые надо распределить по группам, опираясь на информацию, представленную в матрице расстояний между ними. Например, имеется множество объектов (фигуры, расположенные на плоскости, — рис. 2) и следующая симметричная матрица, содержащая значения расстояний между ними по мере d(A,B) = |x_A—x_B|+|y_A—y_B|:

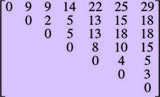
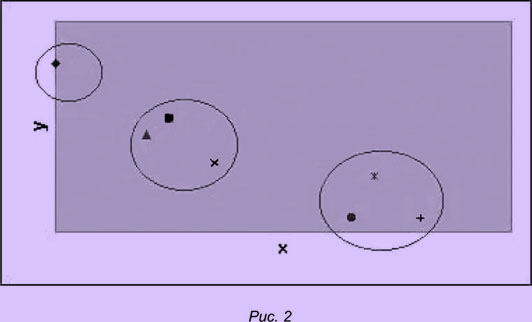
Алгоритм кластеризации должен обнаружить, что можно выделить отдельные группы объектов, а именно:

кластер 1:	объект 1 (¨ );
кластер 2:	объекты 2, 3, 4 (▲ ■ ´ );
кластер 3:	объекты 5, 6, 7 (• +).

В том случае, если мера связи хорошо оценивает смысловые отношения между соответствующими понятиями и если матрица расстояний содержит хорошо подготовленные данные, в результате кластеризации должно быть получено множество групп слов, близких по смыслу.

Формальное описание.

Пусть Ω = (ω_ij) _1≤i,j≤N — матрица расстояний, S={s₁..s_N} — множество стимулов. Необходимо получить кластеры {γ₁..γ_N}.