CLAIM – научно-образовательный кластер

Филиппович Андрей

ВОЗМОЖНОСТЬ ПРИМЕНЕНИЯ И ОСОБЕННОСТИ ПОСТРОЕНИЯ МОДЕЛЕЙ ТЕОРИИ МАССОВОГО ОБСЛУЖИВАНИЯ ДЛЯ ОПИСАНИЯ ПОЛИГРАФИЧЕСКИХ СИСТЕМ

Содержание

Возможность применения ТМО для описания полиграфических систем

Особенности построения аналитических моделей полиграфических систем

Литература

В статье рассматриваются вопросы применения ТМО для описания полиграфических систем. Акцент делается на допечатных процессах. Отмечаются причины неэффективности использования ТМО. Предлагаются решения для преодоления основных ограничений. Рассматриваются вопросы выбора конкретной СМО для описания работы допечатного оборудования.

Возможность применения ТМО для описания полиграфических систем.

Возможность применения теории массового обслуживания для исследования предметной области определяется следующими факторами:

1. Количество заявок в системе (которая рассматривается как СМО) должно быть достаточно велико (массово) [1].

2. Все заявки, поступающие на вход СМО, должны быть однотипными [4].

3. Для расчетов по формулам необходимо знать законы, определяющие поступление заявок и интенсивность их обработки. Более того, потоки заявок должны быть Пуассоновскими [6].

4. Структура СМО, т.е. набор ОА и последовательность обработки заявки, должна быть жестко зафиксирована.

5. Необходимо исключить из системы субъектов или описывать их как ОА с постоянной интенсивностью обработки [8].

К перечисленным выше ограничениям можно добавить еще одно, оказывающее сильное влияние на размерность и сложность математической модели.

6. Количество используемых приоритетов должно быть минимальным. Приоритеты заявок должны быть постоянными, т.е. они не могут меняться в процессе обработки внутри СМО.

Массовость заявок. В работе [2] отмечается следующее: "Анализ полиграфического производства показывает, что теория массового обслуживания может быть использована для анализа различных производственных ситуаций. Первой из них является задача анализа функционирования издательств и типографий как систем массового обслуживания при поступлении в них случайных заявок на издание полиграфической продукции. Заявки могут поступать в случайные моменты времени и могут обладать различной степенью сложности и различным объемом, что приводит к случайному времени исполнения заявок. Применение теории массового обслуживания позволяет оценить пропускную способность издательства или типографии, количество заказов, находящихся в производстве, время пребывания заявок и т.д."

Если рассматривать заказ как заявку в СМО, то количество заказов должно быть массовым. В средних допечатных полиграфических фирмах в среднем обрабатывается около 20 заказов в день. Ежедневный приток новых заказов в среднем составляет не более 25% [7]. Одна печатная машина редко за один день печатает более трех заказов. Аналогичная ситуация возникает и в фирмах, занимающихся послепечатной обработкой [3].

Из выше сказанного следует, что о массовости заказов можно говорить только при рассмотрении продолжительных интервалов времени (недели, месяцы). Для оценки производительности полиграфического предприятия чаще всего достаточно оценить небольшой промежуток времени. В этом случае использование аналитического подхода не оправдано. Для крупных полиграфических корпораций и для фирм, ориентированных на долгосрочные заказы использование ТМО может оказаться более эффективным.

Преодоление ограничения массовости возможно за счет рассмотрения в качестве заявок не заказов, а его составляющих частей. Например, можно представлять заказ как множество страниц.

Однотипность заявок. Проблема однотипности заявок является одним из основных препятствий для использования ТМО в полиграфической предметной области. Многие полиграфисты, считают, что каждый заказ является уникальным, поэтому его нельзя типизировать. Если считать, что заказ имеет более 100 характеристик, каждая их которых может принимать несколько значений, то нельзя не согласиться с этим утверждением.

Преодоление этой проблемы заключается в разбиении заказы на составные части (страницы, технологические операции и др.) и пренебрежении некоторыми характеристиками. Например, задание плотности бумаги, типа и цвета кожи обложки не оказывает серьезного влияния на процесс печати. Параметры заказа, определяющие количество цветов (красок) и формат издания, наоборот, прямо определяют и возможность, и время печати.

В общем случае неучтенные характеристики заказа могут рассматриваться как необходимые ресурсы. Наличие или отсутствие ресурсов может оказывать серьезное влияние на последовательность и время решения задачи. Например, заказы, для которых имеется достаточное количество ресурсов, могут иметь более высокий приоритет. Сложностью такого подхода является то, что приоритеты могут меняться динамически в процессе работы.

Если рассматривать заказ как совокупность технологических операций, на каждую из которых существует норма, то разнородность заявок можно представить в виде нескольких простейших заявок. При этом количество простейших заявок зависит от технологической операции, объема материала и коэффициента сложности.

Еще одной сложностью, вызванной разнородностью, является наличие ОА, которые могут обслуживать только определенные типы заявок. Решение этой проблемы заключается в разделении соответствующих потоков заявок и рассмотрении системы в виде множества независимых последовательно или параллельно связанных СМО. Недостатками этого подхода являются: невозможность точного определения процесса окончания обработки заказа, т.к. заявки привязаны только к технологическим операциям; необходимость генерации и уничтожения заявок на стыках отдельных систем; использование ОА только для обработки одного типа заявок.

Законы поступления заявок. В ТМО, в основном, используются пуассоновские потоки заявок (заказов, технологических операций, компонент заказов). Для расширения области применения ТМО используют различные методы сведения произвольных потоков к пуассоновскому (дифференциальный и интегральный методы, метод Кендалла [5], асимптотические методы [4]). Часто, не зная законы распределения, аналитики рассматривают самые "худшие" случаи, когда число поступающих заявок экспоненциально растет. Однако такой подход позволяет дать только грубую оценку системы.

Для того чтобы определить потоки заявок и интенсивность их обработки необходимо иметь статистические данные. В настоящее время количество исследований в полиграфии на данную тему крайне мало. Единственным источником для анализа полиграфической фирмы может служить собственная статистика, набранная за значительный период времени. Большинство малых и средних фирм оформляют и рассчитывают технологические карты только в бумажном виде. Кроме того, не документируется информация об интенсивности обработки, количестве и причине возникающих ошибок, сложности работы и т.д. Все это служит серьезным препятствиям для использования ТМО.

Фиксированная структура. Для описания системы с помощью ТМО необходимо, чтобы она имела фиксированную структуру и последовательность обработки заявок. Необходимо отметить, что фиксированная последовательность движения заявок не означает полную детерминированность всех процессов обработки. Например, если заявка находится в очереди, которую обслуживают несколько устройств (ОА), то процесс выбора ОА в общем случае является стохастическим. Однако количество ОА для одной очереди, последовательность и направление движение заявок не может меняться.

На практике последовательность выполнения заказа может сильно изменяться. Например, если невозможно осуществить сканирование материалов (Зарезервировать ОА₁) или распечатку исходных данных для вычитки (использовать ОА₂), то можно осуществить ввод данных (ОА₃), верстку (ОА₄) и т.д. Часто один ПК (ОА) используется для выполнения различных технологических операций. При переполнении одной из очередей к ОА, ее необходимо сделать приоритетной, а заявки из других очередей перенаправить в другим ОА. Более того, в классическом представлении к ОА должна иметься только одна очередь. Тогда заявки, размещенные в очередь, должны определенным образом сортироваться либо с помощью динамического изменения приоритетов, либо с помощью других механизмов.

Решением этой проблемы является создание множества математических моделей, фиксация структуры в системе, рассмотрение приближенных случаев. Если количество возможных состояний системы велико, то размерность и сложность математической модели сильно возрастает и использование ТМО не оправдано.

Представление субъектов. Субъекты (персонал) можно представлять в виде ОА с определенной интенсивностью обработки. Их производительность следует определять из статистики, накопленной за продолжительный промежуток времени. Сложностью этого подхода является наличие в производстве новых субъектов (с неизвестной производительностью); постоянное, но неравномерное влияние опыта работника на его производительность; уникальность каждого субъекта.

Альтернативным вариантом задания интенсивности обработки заявки субъектом является использование нормативов. В этом случае математическая модель будет соответствовать "идеальному" производству. Такой подход можно применять для анализа крупных предприятий, где каждый работник выполняет (должен выполнять) один вид работы за фиксированное время. Результатами анализа может являться проверка адекватности нормативов и возможность их изменения.

Часто моделируемую систему исследуют на работоспособность в критических ситуациях: при наличии большого числа заказов, при возникновении большой срочности, при отсутствии или незначительном количестве работы и т.д. В этих случаях поведение субъектов крайне трудно спрогнозировать.

Представление субъектов в полиграфии, особенно, в допечатном производстве имеет специфику. Один сотрудник может выполнять различные виды работы с различным качеством. Отсюда следует, что субъект может обладать вектором специальностей, и для передачи ему работы необходимо оценивать его профессиональные качества и загрузку. Таким образом, переход заявки от одного ОА к другому не является случайным и зависит от многих параметров. Представление зависимостей такого рода в СМО крайне затруднительно.

Приоритеты. Использование приоритетов в полиграфической предметной области необходимо для задания срочности заказов (заявок), для формирования общей очереди к устройствам, выполняющим различные виды работ и т.д. Особенностью использования приоритетов является то, что они могут изменяться динамически в процессе работы. Это связано с тем, что заказы должны выполняться в течение определенного времени, и система должна работать без отказов заявок после их принятия к обработке. Ниже показано, что наличие приоритетов и невозможность отказа от заявки после ее принятия на обработку переводит СМО в разряд замкнутых.

Особенности построения аналитических моделей полиграфических систем.

Рассмотрим построение модели устройств с точки зрения теории массового обслуживания на примере сканера. В большинстве случаев, сканер представляет собой одноканальное устройство, т.е. имеет только один канал обслуживания. Под каналом обслуживания будем понимать возможность выполнения одной задачи.

Будем считать, что обслуживающее устройство (сканер) имеет неограниченное количество источников заявок. На практике, допечатная фирма работает на постоянно изменяющемся рынке заказчиков. Даже если есть небольшое количество постоянных заказчиков, вероятность появления заявки от нового заказчика очень велика. Кроме того, необходимо учитывать большое разнообразие заявок. Следовательно, наиболее походящей моделью является одноканальная разомкнутая СМО.

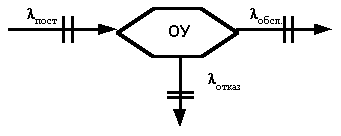
Рис.1. Одноканальная разомкнутая СМО.

Для расчета можно принять, что очередь имеет неограниченный размер. Это означает, что необходимо обслужить все заявки, поступающие в очередь. Каждая заявка должна быть выполнена в определенные сроки, поэтому СМО должна содержать заявки с приоритетами. Приоритеты бывают абсолютные и относительные.

При относительном приоритете требование старшего приоритета, заставшее все каналы обслуживания занятыми, становится в очередь впереди требований младшего приоритета и дожидается освобождения канала.

В случае абсолютного приоритета требование, заставшее каналы занятыми, прерывает обслуживание требования младшего приоритета или становится в очередь, если все каналы обслуживают заявки со старшим приоритетом. Для этого варианта существует три разновидности:

— требование, обслуживание которого прервано, возвращается в очередь, и при возобновлении обслуживания учитывается время, раннее затраченное на обслуживание;

— требование, обслуживание которого прервано, возвращается в очередь, но затраченное время не учитывается, при повторном обслуживании;

— требование младшего приоритета, обслуживание которого прервано, теряется.

На практике, заказы Z для сканирования можно разбить на r составных частей z_i. Каждую часть можно обрабатывать отдельно.

Z = {z₁, z₂, … z_r}

Потеря заявок неприемлема для данной предметной области, т.к. может принести значительные расходы. Относительные приоритеты не позволяют выполнить срочный заказ, если в обслуживании находится большая работа, поэтому остаются два варианта с использованием абсолютных приоритетов. Выбор одного из них зависит от времени выполнения нового заказа T, требуемых для этого ресурсов Res, исполнителя Hu и др. Если процент выполненной работы меньше какого-нибудь критерия Kr, то заявка обслуживается заново полностью.

Zi/Z < Kr, Kr = func (T, Res, Hu …),

где Zi — доля выполненной работы.

Основная сложность математической модели такой СМО заключается в том, что заявка с малым приоритетом может быть не обслужена. Для избежания таких ситуаций необходимо менять приоритеты во время обслуживания.

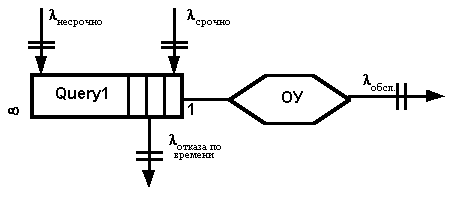
Рис.2. Одноканальная разомкнутая СМО с бесконечной очередью
и ограничением по времени.

Главным критерием для выставления приоритетов, как отмечалось выше, является время выполнения заказа. Отсюда следует, что нужно использовать СМО с ограниченным временем ожидания (рис. 2).

В рассматриваемой СМО не должно быть отказов, а это значит, что поток отказов по времени выполнения заявки l_{отк.ввз.}, нужно перенаправить и добавить в поток срочных заказов l_срочно (рис. 3). В результате этих операций получится суммарный поток lе _срочно. Объединение потоков, переводит СМО в разряд замкнутых.

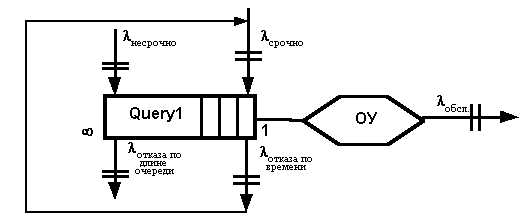
Рис.3. Замкнутая одноканальная СМО с бесконечной очередью
и ограничением по времени.

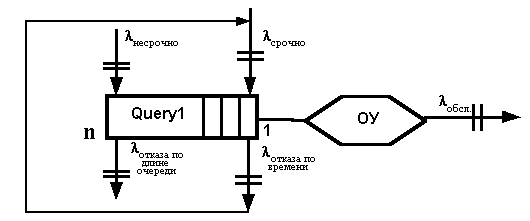
Рис.4. Замкнутая одноканальная СМО с ограниченной очередью,
и ограничением по времени.

Такая схема организации требует ограничения очереди таким образом, чтобы все заказы были выполнены вовремя. Размер очереди в этом случае уменьшится и будет равен n. Это приведет к появлению потока отказов по длине очереди l_отк.до (рис.4). Если в системе имеется несколько типов приоритетов, то схема СМО значительно усложнится.

Итак, можно сделать вывод, что очередь должна быть конечной, из-за того, что в ней есть приоритеты, ограничение во времени и необходимость обслужить все заявки. Построение аналитической модели с приоритетами очень сложно, особенно если их более двух. Для упрощения математической модели можно воспользоваться одноканальной разомкнутой СМО с ограниченной очередью, размером m.

Основными параметрами этой модели СМО являются абсолютная пропускная способность А (число заявок в единицу времени) и вероятность отказа заявки P_отк.

P_отк = [(l/r)^m+1(1 – l/r)] / [1 – (l/r)^m+2]

A = l (1 - P_отк) = l (1 - [ (l/r)^m+1(1 – l/r) ] / [1 – (l/r)^m+2 ]),

где l — интенсивность поступления заявок;

r — интенсивность обслуживания заявок.

Средняя длина очереди (количество элементов, ожидающих обслуживания) w, среднее время ожидания заявки в очереди T_w и время пребывания заявки в СМО T_q являются важными характеристиками для СМО с очередями.

w = (l/r)² {1 – (l/r)^m[m+1–m(l/r)]}/ [1 – (l/r)^m+2 ](1 – l/r)

T_w = w / l

T_q = T_w + A/lr

Возникает закономерный вопрос о соотношении длин очередей n и m. Оно зависит от процентного содержания работ с разными приоритетами и от времени их выполнения.

Для простоты вычислений положим, что существует два типа приоритетов заказов. Введем некий коэффициент x , который характеризует соотношение между потоками срочных (lе _срочно) и несрочных заказов (l_{несрочно}).

x = (lе _срочно)/ (l_{несрочно}) (*)

(lе _срочно) = x (l_{несрочно})

Чтобы обеспечить эффективность работы, время обработки всех заказов должно быть больше, чем интенсивность заявок, т.е.

1/r < 1/( lе _срочно + l_{несрочно})

( lе _срочно + l_{несрочно}) < r

Подставляя в это соотношение формулу (*), можно получить, что

lе _срочно < r*x / (x +1)

l_{несрочно}< r / (x +1)

Если известен оптимальный коэффициент x и интенсивность обработки заявок за единицу времени, то можно найти ограничения для потоков и соотношение между ними.

Попробуем оценить коэффициент x . Очевидно, что чем больше срочных заказов, тем меньше должна быть длина очереди. Следовательно, коэффициент обратно пропорционален длине очереди.

x ~ 1/n => x =k/n => n₁= k₁*n_50/50/x , k= k₁*n_50/50

где k — коэффициент пересчета длины очереди;

k₁ — коэффициент соответствия. Он определяется законами распределения поступления и обработки заявок;

n_50/50 — длина очереди при наличии 50% срочных и 50% несрочных заявок;

n₁ — новое значение длины очереди.

Если исходить из длины очереди n_неср., в которой все заявки несрочные, то формула примет следующий вид:

n₁= k₁* n_неср./(x +1),

На рис.5. приведен график, иллюстрирующий зависимость длины очереди от коэффициента x .

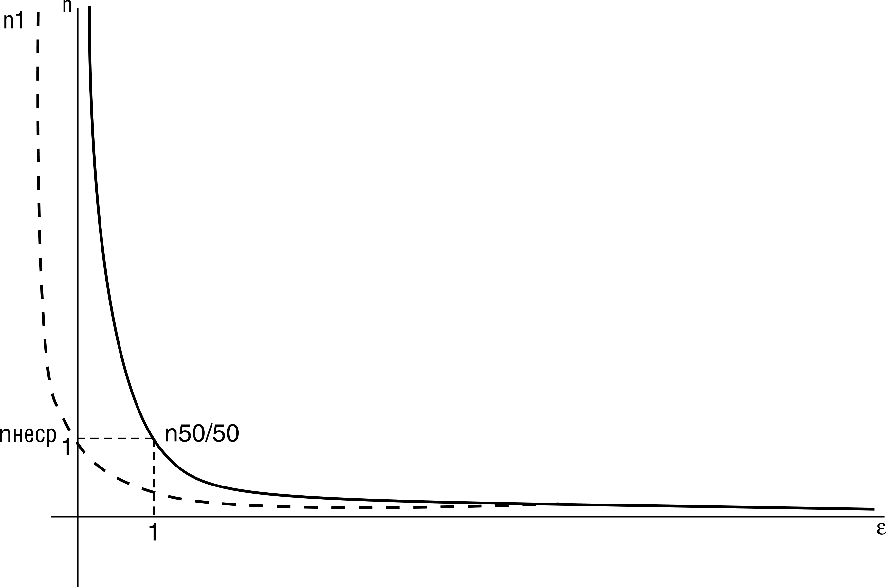
Рис.5. График зависимости длины очереди от коэффициента x .

Рассмотрим предельные случаи:

При x ® Ґ , n® 0 очередь будет отсутствовать. Если используется два типа приоритетов, то граф переходов СМО будет иметь вид, представленный на рис.6. На вход поступают два независимых потока заявок l₁ и l₂. Требования первого потока обладают старшим абсолютным приоритетом.

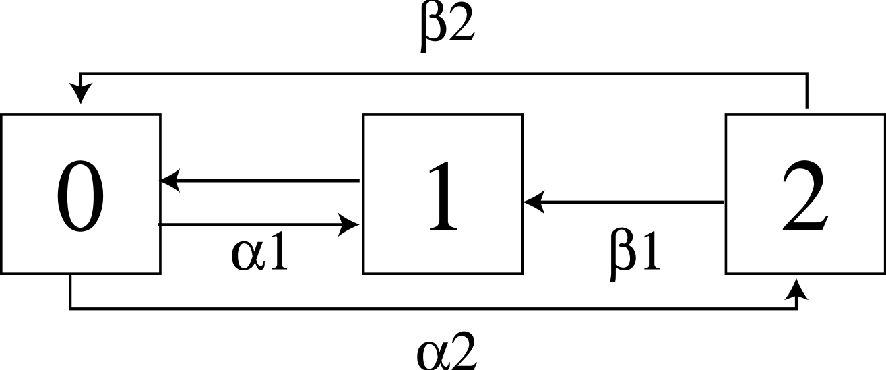
Рис.6. Граф переходов СМО с отказами и двумя приоритетами.

Очередь отсутствует, поэтому заявка младшего приоритета, обслуживание которой прервано, теряется. Теряется также и заявка старшего приоритета, когда канал занят обслуживанием заявки этого же приоритета. Вероятность потери заявки P_пот определяется следующей формулой:

P_пот = [l₁(l₁ + l₂ +r₂) + r₁(l₁ + l₂)] / [(l₁ + l₂) (l₁ + l₂ +r₂)]

Если рассматривать заявки без приоритетов, то получится одноканальная СМО с отказами. Особенностью данной модели является работа без очереди, т.е. если заявка не может быть обслужена, она отбрасывается и в дальнейшей работе не участвует.

Такая ситуация вполне возможна для рынка полиграфических услуг. Например, имеется очень большое (для расчетов можно принять бесконечное) количество заказов. Тогда отсутствует необходимость создавать очередь. Такие ситуации могут возникать лишь на небольшие промежутки времени во время сильного роста спроса. Работать по такой схеме не очень выгодно, т.к. можно потерять постоянных заказчиков.

A = lr/(l+r)

P_отк = l/(l+r)

При x ® 0, n® Ґ очередь неограниченно возрастает, и модель системы приближается к одноканальной СМО с неограниченной очередью. Установившийся режим работы СМО может быть только в случае, когда интенсивность входного потока не больше интенсивности обслуживания.

l/r <=1

Пропускная способность будет равняться интенсивности входного потока, а среднее число заявок в очереди m_k будет одной из важнейших характеристик данной СМО.

A = l

m_k = (l/r)² /(1-l/r)

При конкретных значениях, например, x =20%, и притом, что суммарное время обработки срочных и несрочных заявок остается постоянным, длина очереди уменьшится почти на 20%. Данный расчет приблизительный и не учитывает законы распределения случайного появления заявок.

x =20%, ( lе _срочно + l_{несрочно}) = const, k₁=1 => n₁=1/1.2=0.83

Если подвести итог построению аналитических моделей допечатного оборудования, то можно сделать следующие выводы:

— Для расчета аналитической модели требуются сложные математические вычисления.

— Аналитические модели трудноизменяемы и не наглядны. Приближенные модели сильно типизированы и не позволяют учесть особенности устройств и работы с ними.

— Чтобы избежать этих недостатков, можно воспользоваться альтернативным вариантом и построить имитационную модель.

Литература:

 © НОК CLAIM, 2006-2012. Замечания, вопросы и сведения об ошибках просим сообщать в форуме или присылать администратору сайта.