CLAIM – научно-образовательный кластер

Лабораторная работа "Генетические алгоритмы"

Миляев Николай, гр. ИУ5-81

1. Условие задачи

«Спортсмен-ориентировщик должен пробежать по всем контрольным пунктам по одному разу и прибежать к финишу. В таблице, задаваемой пользователем, задаётся условное время прохождения от одного пункта к другому (топология сети маршрутов).

Необходимо определить самый быстрый маршрут прохождения дистанции.»

Пользователь при решении задачи задаёт таблицу маршрутов (для облегчения его задачи таблица заполняется случайными числами). На пересечении i-й строки и j-го столбца находится время прохождения маршрута от i-го пункта к j-му (j<i), или от j-го пункта к i-му (время прохождения отрезка дистанции не зависит от направления бега). Время задаётся целым положительным числом от 1 до 999.

Маршрут спортсмена должен начинаться в 0-м пункте («старт») и заканчиваться в 9-м («финиш»). Он записывается в виде восьми неповторяющихся цифр, например, 87436125 (что означает, что спортсмен прибегает со старта на 8-й пункт, потом с 8-го на 7-й, с 7-го на 4-й, и т. д., со 2-го на 5-й, с 5-го бежит к финишу). Время прохождения дистанции равно сумме времени прохождения всех 9 отрезков.

Также пользователь задаёт несколько параметров, влияющих на работу алгоритма: максимальное число итераций и максимальное число итераций, в ходе которых не было достигнуто улучшение наилучшего маршрута, размер популяции (выборки маршрутов) и вероятность мутации (непредсказуемого изменения маршрута).

2. Используемые технологии

Программа написана на языке PHP и построена на основе Web-технологий. Для её работы требуется следующее ПО:

• На сервере — ОС Linux, Web-сервер Apache, PHP 5-й версии (возможна работа с другими ОС и Web-серверами, тестирование не проводилось).

• На клиенте — любой Web-браузер (на клиентской стороне используется только HTML).

Так как программа построена на основе Web-технологий, она может быть доступной через сеть Интернет. Для запуска программы нажмите на эту ссылку.

Так как программа может быть вызвана любым пользователем Интернета, возможно, в автоматическом режиме, и может потреблять при выполнении много ресурсов сервера, она должна иметь средства защиты от DoS атак (иначе злонамеренный пользователь может перегрузить сервер, послав большое число запросов к странице с программой). В данной программе используется сохранение временной метки во временный файл и последующее считывание этой метки. Программа может запускаться не чаще 1 раза в 20 секунд (значение может быть изменено).

В программе используется классический генетический алгоритм, приведённый в лекции (см. раздел 4) с незначительными изменениями.

3. Алгоритм решения задачи

Схема алгоритма решения задачи представлена на рис. 1.

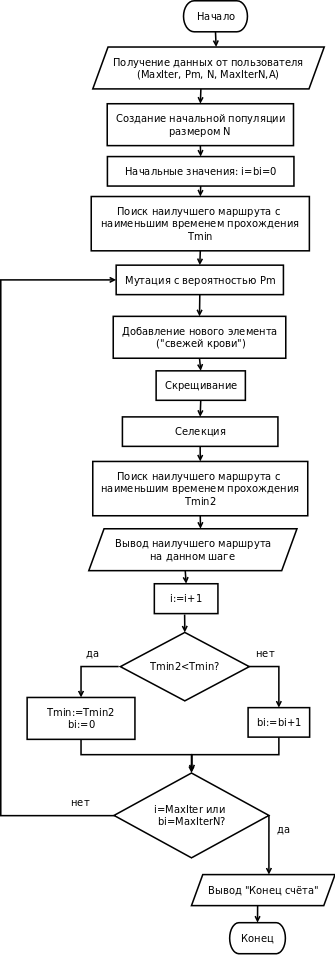
Рис. 1. Блок-схема алгоритма программы.

К числу операторов генетического алгоритма относятся операторы мутации, скрещивания и селекции. С целью повышения разнообразия был добавлен оператор добавления нового элемента, который можно рассматривать как разновидность оператора мутации.

Элементами или особями популяции являются маршруты прохождения дистанции. Они представлены в виде строки из 8 неповторяющихся цифр от 1 до 8, например, «31754826». Функция определения расстояния просматривает заданную пользователем матрицу времени прохождения отрезков маршрута А, выбирает из неё время прохождения каждого из 9 отрезков дистанции, и возвращает время прохождения дистанции — сумму времён прохождения каждого из отрезков. Если время прохождения отрезка дистанции между двумя пунктами не задано, то программа рассматривает это как отсутствие пути, и присваивает такому отрезку достаточно большое время прохождения, равное 100000.

Популяция создаётся в виде массива, включающего в себя заданное число строк из случайно перемешанных цифр от 1 до 8.

Оператор мутации с заданной вероятностью меняет местами 2 цифры в строке. Оператор мутации не применяется к первому (наилучшему) элементу популяции.

Оператор добавления нового элемента добавляет в популяцию один элемент в виде строки из случайно перемешанных цифр от 1 до 8, который будет участвовать в скрещивании.

Оператор скрещивания работает следующим образом: Вычисляется сумма величин, обратно пропорциональных времени прохождения дистанции:

(здесь коэффициент К — некая константа)

Элемент s_i, выбранный с вероятностью p_i, скрещивается с элементом s_j, выбранным с вероятностью p_{j .} Вероятность выбора вычисляется по формуле:

Вероятность выбора маршрута обратно пропорциональна времени его прохождения.

В ходе скрещивания двух элементов производится отделение от первого родителя на части случайной длины (от 1 до 7 цифр), и дополнение её теми цифрами из строки второго родителя, которых нет в строке первого, с сохранением порядка. Например, при скрещивании элементов «12345678» и «87654321» может получиться «12348765» или «18765432». Скрещивание проводится столько раз, сколько элементов в популяции (размер популяции удваивается).

В ходе выполнения оператора селекции происходит удаление повторяющихся элементов из популяции, популяция сортируется, и от неё остаётся только заданное в качестве размера популяции число элементов (если за счёт большого числа повторяющихся элементов размер популяции стал меньше заданного, то она дополняется новыми случайно сгенерированными элементами).

Если в течение заданного числа итераций (включающих в себя операторы мутации, скрещивания и селекции) не произошло уменьшения наименьшего времени прохождения дистанции, или достигнут предел общего количества итераций, программа выводит результат (может ли спортсмен пройти дистанцию или нет). Спортсмен может пройти дистанцию, если его маршрут включает только проходимые участки, т.е время прохождения маршрута не превышает условного достаточно большого времени прохождения непроходимого участка - 100000 единиц времени).

4. Результаты экспериментов

Эксперименты с программой проводились на случайно сгенерированном примере следующего вида:

В таблице 1 представлены результаты 10 запусков программы при следующих параметрах:

1. Параметры по умолчанию (вероятность мутации 0.001, максимальное общее число итераций 25, максимальное число итераций без улучшения 10, размер популяции 10).

2. Большая вероятность мутации 0.2.

3. Большое число итераций (общее — 250, без улучшения — 100)

4. Большой размер популяции (50).

5. Вероятность мутации равна единице (для всех элементов, кроме наилучшего)

Результаты приведены только для успешного прохождения дистанции.

Таблица 1. Результаты запусков программы.

Для точного решения задачи можно использовать программу lp_solve, предназначенную для решения задач линейного программирования. Создаётся описание следующей задачи (конечно, это удобнее делать не вручную, а с использованием программных средств):

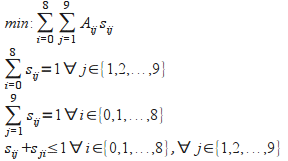
Здесь A_ij — матрица расстояний от i-го пункта до j-го, s_ij — двоичные переменные (принимающие значения 0 или 1), показывающие включение в маршрут отрезка от пункта номер i до пункта номер j.

С первого раза может получиться неправильное решение, при котором маршрут разбивается на две несвязные части. Тогда к задаче нужно добавить ограничение вида

для такой несвязной части.

Время решения составляет приблизительно 10 миллисекунд. Программа lp_solve использует метод ветвей и границ.

Конечно, можно проверить и прямым перебором всех 8! = 40320 вариантов маршрута, но такой способ не использует эвристические методы и малопригоден при большем количестве пунктов.

Оказалось, что самый оптимальный маршрут для данной задачи имеет вид 76582143 и время прохождения 214 единиц. Он несколько раз встречался в результатах запуска программы. Важная особенность генетических алгоритмов заключается в том, что нельзя сказать, является ли найденное решение самым оптимальным.

5. Выводы по результатам экспериментов

1. Генетический алгоритм находит не обязательно самый оптимальный вариант решения, а лишь достаточно близкий к нему.

2. Генетический алгоритм может и не найти приемлемого решения.

3. Повышение частоты мутаций (до определённого предела) повышает качество получаемого решения при небольшом увеличении времени вычисления.

4. Слишком большая частота мутаций приводит к снижению качества решения за счёт ухудшения признаков «хороших» особей.

5. Повышение числа итераций снижает разброс получаемых решений.

6. Увеличение размера популяции приводит к наибольшему качеству получаемых решений, но связано с наибольшими вычислительными затратами.

 © НОК CLAIM. Замечания, вопросы и сведения об ошибках просим сообщать в форуме или присылать администратору сайта.